练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，正方体ABCD－A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′分别交于M，N两点，设BM＝x，x∈[0,1]，给出以下四个结论：

    ①平面MENF⊥平面BDD′B′；

    ②直线AC∥平面MENF始终成立；

    ③四边形MENF周长L＝f(x)，x∈[0,1]是单调函数；

    ④四棱锥C′－MENF的体积V＝h(x)为常数；

    以上结论正确的是__________．

    【答案】①②④

    【解析】连接，则，而，又平面， 平面， ，所以， ，由，所以平面 ， 平面，故平面 ，①正确；由前述证明可知平面， 平面，故平面，②也成立；四边形为菱形， ，它不是单调函数，故③错； ， 到平面的距离为1， ，故为定值．故填①②④．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】据统计，目前微信用户已达10亿，2016年，诸多传统企业大佬纷纷尝试进入微商渠道，让这个行业不断地走向正规化、规范化.2017年3月25日，第五届中国微商博览会在山东济南舜耕国际会展中心召开，力争为中国微商产业转型升级，某品牌饮料公司对微商销售情况进行中期调研，从某地区随机抽取6家微商一周的销售金额（单位：百元）的茎叶图如图所示，其中茎为十位数，叶为个位数.

    （1）若销售金额（单位：万元）不低于平均值的微商定义为优秀微商，其余为非优秀微商，根据茎叶图推断该地区110家微商中有几家优秀？

    （2）从随机抽取的6家微商中再任取2家举行消费者回访调查活动，求恰有1家是优秀微商的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆右顶点与右焦点的距离为，短轴长为

    （I）求椭圆的方程；

    （Ⅱ）过左焦点F的直线与椭圆分别交于A、B两点，若三角形OAB的面积为求直线AB的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

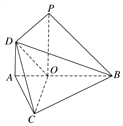
    【题目】如图，在△ABC中，∠ABC＝45°，点O在AB上，且OB＝OC＝AB，PO⊥平面ABC，DA∥PO，DA＝AO＝PO.

    (1)求证：PB∥平面COD；

    (2)求二面角O－CD－A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种产品的质量以其质量指标值衡量，并依据质量指标值划分等级如下表：

    从某企业生产的这种产品中抽取200件，检测后得到如下的频率分布直方图：

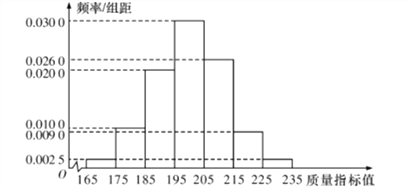
    (1)根据以上抽样调查数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品”的规定？

    (2)在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一、二、三等品都有的概率；

    (3)该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值近似满足，则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

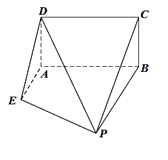
    【题目】如图，已知矩形所在平面垂直于直角梯形所在平面于直线，且， 且∥．

    （Ⅰ）设点为棱中点，求证： 平面；

    （Ⅱ）线段上是否存在一点，使得直线与平面所成角的正弦值等于？若存在，试确定点的位置；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    (1)证明: 图象恒在直线的上方;

    (2)若在恒成立,求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2016·云南玉溪一中月考)已知函数，函数g(x)＝f(x)－x＋1的零点按从小到大的顺序排列成一个数列，该数列的前n项的和为Sn，则S10等于(　　)

    A. 45 B. 55

    C. 210－1 D. 29－1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥中,棱底面,且, , , 是的中点.

    (1)求证: 平面；

    (2)求三棱锥的体积.

    查看答案和解析>>

    同步练习册答案