
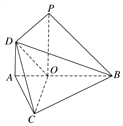
【题目】如图,在△ABC中,∠ABC=45°,点O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求证:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
【答案】(1)见解析;(2) ![]()
【解析】试题分析:(1)利用平几知识计算可得OD∥PB,再根据线面平行判定定理得结论(2)过A作AM⊥DO,垂足为M,过M作MN⊥CD于N,则根据二面角定义得∠ANM为二面角O-CD-A的平面角.再解三角形可得二面角O-CD-A的余弦值.
试题解析:(1)证明 因为PO⊥平面ABC,DA∥PO,AB平面ABC,
所以PO⊥AB,DA⊥AB.
又DA=AO=![]() PO,所以∠AOD=45°.
PO,所以∠AOD=45°.
因为OB=![]() AB,
AB,
所以OA=![]() AB,所以OA=
AB,所以OA=![]() OB,
OB,
又AO=![]() PO,所以OB=OP,
PO,所以OB=OP,
所以∠OBP=45°,即OD∥PB.
又PB平面COD,OD平面COD,
所以PB∥平面COD.
(2)解 如图,过A作AM⊥DO,垂足为M,
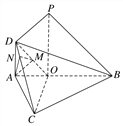
过M作MN⊥CD于N,连接AN,
则∠ANM为二面角O-CD-A的平面角.设AD=a,
在等腰直角三角形AOD中,得AM=![]() a,
a,
在直角三角形COD中,得MN=![]() a,
a,
在直角三角形AMN中,得AN=![]() a,
a,
所以cos∠ANM=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=![]() ,n=
,n=![]() ,现有如下命题:
,现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中真命题有___________________(写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x(1-![]() )是R上的偶函数.
)是R上的偶函数.
(1)对任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求实数m的取值范围.
≥2x+1恒成立,求实数m的取值范围.
(2)令g(x)=1-![]() ,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
,设函数F(x)=g(4x-n)-g(2x+1-3)有零点,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 在点(1,1)处的切线方程为x+y=2.
在点(1,1)处的切线方程为x+y=2.
(1)求a,b的值;
(2)对函数f(x)定义域内的任一个实数x,不等式f(x)-![]() <0恒成立,求实数m的取值范围.
<0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.
(1)求证:BE1⊥DC;
(2)求证:DM∥平面BCE1;
(3)判断直线CD与ME1的位置关系,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线EF的平面分别与棱BB′、DD′分别交于M,N两点,设BM=x,x∈[0,1],给出以下四个结论:

①平面MENF⊥平面BDD′B′;
②直线AC∥平面MENF始终成立;
③四边形MENF周长L=f(x),x∈[0,1]是单调函数;
④四棱锥C′-MENF的体积V=h(x)为常数;
以上结论正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学每年暑假举行“学科思维讲座”活动,每场讲座结束时,所有听讲这都要填写一份问卷调查.2017年暑假某一天五场讲座收到的问卷份数情况如下表:
学科 | 语文 | 数学 | 英语 | 理综 | 文综 |
问卷份数 |
|
|
|
|
|
用分层抽样的方法从这一天的所有问卷中抽取![]() 份进行统计,结果如下表:
份进行统计,结果如下表:
满意 | 一般 | 不满意 | |
语文 |
|
|
|
数学 |
| 1 |
|
英语 |
|
|
|
理综 |
|
|
|
文综 |
|
|
|
(1)估计这次讲座活动的总体满意率;
(2)求听数学讲座的甲某的调查问卷被选中的概率;
(3)若想从调查问卷被选中且填写不满意的人中再随机选出![]() 人进行家访,求这
人进行家访,求这![]() 人中选择的是理综讲座的人数的分布列.
人中选择的是理综讲座的人数的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com