
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
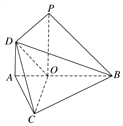
【题目】如图,在△ABC中,∠ABC=45°,点O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求证:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面于直线
所在平面于直线![]() ,且
,且![]() ,
, ![]() 且
且![]() ∥
∥![]() .
.
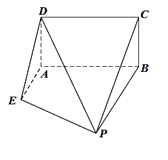
(Ⅰ)设点![]() 为棱
为棱![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·云南玉溪一中月考)已知函数![]() ,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
,函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,该数列的前n项的和为Sn,则S10等于( )
A. 45 B. 55
C. 210-1 D. 29-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,现在每招聘一名教师需要1万元,若三年后教师严重短缺时再招聘,由于各种因素,则每招聘一名教师需要3万元,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:
流失教师数 | 6 | 7 | 8 | 9 |
频数 | 10 | 15 | 15 | 10 |
以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率,记![]() 表示两所县乡中学在过去三年共流失的教师数,
表示两所县乡中学在过去三年共流失的教师数, ![]() 表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
表示今年为两所县乡中学招聘的教师数.为保障县乡孩子教育不受影响,若未来三年内教师有短缺,则第四年马上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(3)以未来四年内招聘教师所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com