
| A. | $y=sin(4x-\frac{π}{5})$ | B. | $y=sin(2x-\frac{2π}{5})$ | C. | $y=sin(4x-\frac{2π}{5})$ | D. | $y=sin(4x-\frac{3π}{5})$ |
分析 根据函数y=Asin(ωx+φ)的图象变换规则对函数的解析式进行变换即可,由题设条件知,本题的变换涉及到了平移变换,周期变换,振幅变换.
解答 解:由题意函数y=sin(2x-$\frac{π}{5}$)的图象上各点向右平移$\frac{π}{5}$个单位长度,
得到y=sin(2x-$\frac{2π}{5}$-$\frac{π}{5}$)=sin(2x-$\frac{3π}{5}$),
再把横坐标缩短为原来的一半,
所得图象的表达式是:y=sin(4x-$\frac{3π}{5}$).
故选:D.
点评 本题考查函数y=Asin(ωx+φ)的图象变换,求解的关键是准确熟练掌握函数y=Asin(ωx+φ)的图象变换规则,三角函数的图象变换是三角函数中的重要内容,一定要注意总结其规律.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题
 在直三棱柱ABC-A1B1C1中,若BC⊥AC,$∠A=\frac{π}{3}$,AC=4,AA1=4,M为AA1的中点,P为BM的中点,Q在线段CA1上,A1Q=3QC.则异面直线PQ与AC所成角的正弦值为( )
在直三棱柱ABC-A1B1C1中,若BC⊥AC,$∠A=\frac{π}{3}$,AC=4,AA1=4,M为AA1的中点,P为BM的中点,Q在线段CA1上,A1Q=3QC.则异面直线PQ与AC所成角的正弦值为( )| A. | $\frac{{\sqrt{39}}}{13}$ | B. | $\frac{{2\sqrt{13}}}{13}$ | C. | $\frac{{2\sqrt{39}}}{13}$ | D. | $\frac{{\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
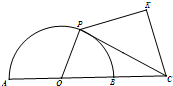 如图,已知半圆O的半径为1,点C在直径AB的延长线上,且BC=1,P是半圆上动点,以PC为一边作等腰直角三角形PCK(K为直角顶点,且K和O在PC的两侧).
如图,已知半圆O的半径为1,点C在直径AB的延长线上,且BC=1,P是半圆上动点,以PC为一边作等腰直角三角形PCK(K为直角顶点,且K和O在PC的两侧).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\sqrt{\frac{{\sqrt{5}+1}}{2}}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=$\sqrt{2}$,AB=BC=1,AD=2,E为PD中点.
如图所示的四棱锥P-ABCD中,已知PA⊥平面ABCD,AD∥BC,∠BAD=90°,PA=$\sqrt{2}$,AB=BC=1,AD=2,E为PD中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com