（本小题满分13分）
设
的BC边上的高AD=BC，a，b，c分别是内角A，B，C的对边。
（1）求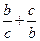
的最小值及取得最小值时
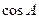的值；
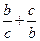（2）把表示为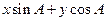
的形式，判断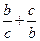能否等于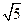
？并说明理由。
科目：高中数学 来源： 题型：解答题
某海滨浴场的岸边可以近似的看成直线，位于岸边A处的救生员发现海
中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D
处，然后游向B处.若救生员在岸边的行进速度是6米/秒，在海中的行进速度是2米/秒.
（不考虑水流速度等因素）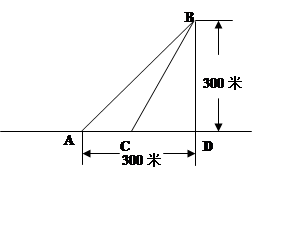
（1）请分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间最短，并求出最短时间.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
在一个特定时段内，以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东
且与点A相距40
海里的位置B，经过40分钟又测得该船已行驶到点A北偏东+
(其中sin=
，
)且与点A相距10
海里的位置C.
(1)求该船的行驶速度（单位：海里/小时）;
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＋
，当且仅当
时，即三角形是等腰三角形时，
，
…………………………5分
，
，
…………………………9分
，其中
，当且仅当
，即
时，
同时成立，所以a是最小的边，
，所以
。
，所以
，
的最大值和最小正周期；
的内角
的对边分别
且
,
，若
,求
的值．
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
．
的值；
中，内角
，
，
对边的边长分别是
，已知
．
，求
，
；
，求△
的内角
、
的对边分别为
、
，
，
.
；
，求
，c=1，
，求a，A，C．