
已知直线l过点P(2,0),斜率为 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
(1)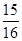 ;(2)
;(2)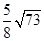
解析试题分析:(1)写出过点P(2,0)的直线方程的参数方程,联立抛物线的方程得到一个含参数t二次方程.通过韦达定理即定点到中点的距离可得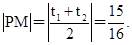 故填
故填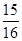 .
.
(2)弦长公式|AB|=|t2-t1|再根据韦达定理可得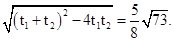 故填
故填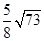 .本题主要知识点是定点到弦所在线段中点的距离.弦长公式.这两个知识点都是参数方程中的长测知识点.特别是到中点的距离的计算要理解清楚.
.本题主要知识点是定点到弦所在线段中点的距离.弦长公式.这两个知识点都是参数方程中的长测知识点.特别是到中点的距离的计算要理解清楚.
试题解析:(1)∵直线l过点P(2,0),斜率为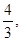
设直线的倾斜角为α,tanα=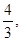 sinα=
sinα=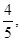 cosα=
cosα=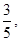
∴直线l的参数方程为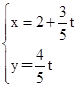 (t为参数)(*) 1分
(t为参数)(*) 1分
∵直线l和抛物线相交,将直线的参数方程代入抛物线方程y2=2x中,整理得
8t2-15t-50=0,且Δ=152+4×8×50>0,
设这个一元二次方程的两个根为t1、t2,
由根与系数的关系,得t1+t2=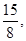 t1t2=
t1t2=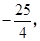 3分
3分
由M为线段AB的中点,根据t的几何意义,
得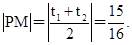 4分
4分
(2)|AB|=|t2-t1|
=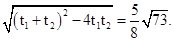 7分
7分
考点:1.直线的参数方程的表示.2.定点到中的距离公式.3.弦长公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知在直角坐标系xOy中,曲线C的参数方程为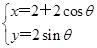 (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin 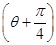 =2
=2 .
.
(1)求曲线C在极坐标系中的方程;
(2)求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线C1的参数方程为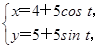 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系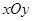 中,
中, 是过定点
是过定点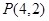 且倾斜角为
且倾斜角为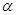 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点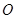 为极点,以
为极点,以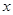 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线 的极坐标方程为
的极坐标方程为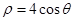 .
.
(I)写出直线 的参数方程;并将曲线
的参数方程;并将曲线 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(II)若曲线 与直线相交于不同的两点
与直线相交于不同的两点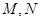 ,求
,求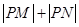 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系 中,曲线
中,曲线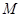 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点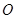 为极点,
为极点, 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为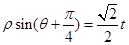 (其中
(其中 为常数).
为常数).
(1)若曲线 与曲线
与曲线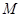 只有一个公共点,求
只有一个公共点,求 的取值范围;
的取值范围;
(2)当 时,求曲线
时,求曲线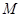 上的点与曲线
上的点与曲线 上的点的最小距离
上的点的最小距离
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知极坐标系的极点为直角坐标系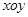 的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线
的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同,已知曲线 的极坐标方程为
的极坐标方程为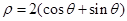 .
.
(Ⅰ)求 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线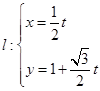 (
(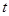 为参数)与曲线C交于
为参数)与曲线C交于 ,
, 两点,与
两点,与 轴交于
轴交于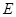 ,求
,求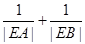 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
已知直线l经过点P(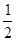 ,1),倾斜角
,1),倾斜角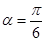 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为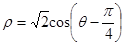 。
。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
(坐标系与参数方程选讲选做题)
已知圆 的参数方程为
的参数方程为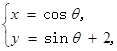
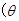 为参数), 以原点为极点,
为参数), 以原点为极点,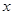 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线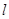 的极坐标方程为
的极坐标方程为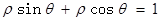 , 则直线
, 则直线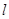 截圆
截圆 所得的弦长是 .
所得的弦长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com