
分析 (1)由正弦定理得到:sinA=sinCsinB+sinBcosC,从而cosBsinC=sinCsinB,由此能求出A+C的值.
(2)由余弦定理得到:b2=a2+c2-2accosB,从而$ac≤\frac{2}{{2-\sqrt{2}}}=2+\sqrt{2}$,当且仅当$a=c=\sqrt{2+\sqrt{2}}$时“=”成立,由此能求出△ABC面积的最大值.
解答 解:(1)由正弦定理得到:sinA=sinCsinB+sinBcosC
因为在三角形中,sinA=sin[π-(B+C)]=sin(B+C)
所以sin(B+C)=sinBcosC+cosBsinC=sinCsinB+sinBcosC
所以cosBsinC=sinCsinB
因为C∈(0,π),sinC≠0,所以cosB=sinB即tanB=1,B∈(0,π)
所以$B=\frac{π}{4}$即$A+C=\frac{3}{4}π$.
(2)由余弦定理得到:b2=a2+c2-2accosB,所以$2={a^2}+{c^2}-\sqrt{2}ac$,
所以$2+\sqrt{2}ac={a^2}+{c^2}≥2ac$即$ac≤\frac{2}{{2-\sqrt{2}}}=2+\sqrt{2}$
当且仅当a=c即$a=c=\sqrt{2+\sqrt{2}}$时“=”成立,
而${S_{△ABC}}=\frac{1}{2}acsinB=\frac{{\sqrt{2}}}{4}ac$,
所以△ABC面积的最大值为$\frac{{1+\sqrt{2}}}{2}$.
点评 本题考查三角形两个内角和的求法,考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意正弦定理、余弦定理的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:解答题
如图,在梯形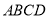 中,
中, ,平面
,平面 平面
平面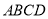 ,四边形
,四边形 是矩形,
是矩形, ,点
,点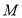 在线段
在线段 .
.

(1)求证: 平面
平面 ;
;
(2)当 为何值时,
为何值时, 平面
平面 ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(文)试卷(解析版) 题型:选择题
若双曲线 (
( )的左、右焦点分别为
)的左、右焦点分别为 被抛物线
被抛物线 的焦点分成
的焦点分成 的两段,则双曲线的离心率为( )
的两段,则双曲线的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com