
���� ��1���Ƚ�C1�IJ������̻�Ϊ��ͨ���̣��ٻ�Ϊ�����귽�̣���C2�ļ����귽������ͬ�˦ѣ����ݼ�������ֱ������Ķ�Ӧ��ϵ�ó�C2��ֱ�����귽�̣�
��2�����l�IJ������̣��ֱ����C1��C2����ͨ���̣����ݲ����ļ�������ó�|OA|��|OB|���õ�|OA|•|OB|����k�ĺ���������k�ķ�Χ�ó��𰸣�
��� �⣺��1������C1��ֱ�����귽��Ϊ��x-1��2+y2=1����x2+y2-2x=0��
������C1�ļ����귽��Ϊ��2-2��cos��=0������=2cos�ȣ�
������C2�ļ����귽��Ϊ��cos2��=sin�ȣ�����2cos2��=��sin�ȣ�
������C2��ֱ�����귽��Ϊx2=y��
��2��������l����б��Ϊ����
������l�IJ�������Ϊ$\left\{\begin{array}{l}{x=tcos��}\\{y=tsin��}\end{array}\right.$��tΪ������$\frac{��}{4}������\frac{��}{3}$����
������l�IJ������̴�������C1����ͨ���̵ã�t2-2tcos��=0��
���t1=0��t2=2cos����
��|OA|=|t2|=2cos����
������l�IJ������̴�������C2����ͨ���̵ã�cos2��t2=tsin����
���t1=0��t2=$\frac{sin��}{co{s}^{2}��}$��
��|OB|=|t2|=$\frac{sin��}{co{s}^{2}��}$��
��|OA|•|OB|=2cos��•$\frac{sin��}{co{s}^{2}��}$=2tan��=2k��
��k�ʣ�1��$\sqrt{3}$]����2k�ʣ�2��2$\sqrt{3}$]��
��|OA|•|OB|��ȡֵ��Χ�ǣ�2��2$\sqrt{3}$]��
���� ���⿼���˲������̣������귽������ͨ���̵�ת���������ļ��������Ӧ�ã������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017��ӱ���ˮ��ѧ������ѧ�ڵ���������ѧ�������Ծ��������棩 ���ͣ������
��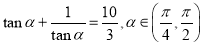 ����
����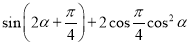 ��ֵΪ___________��
��ֵΪ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{2}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{4}{3}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
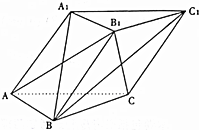 ��ͼ����֪������ABC-A1B1C1�У�����A1ACC1�͵���ABC������߳��IJ��ⳤ��Ϊ2��A1B=$\sqrt{6}$��
��ͼ����֪������ABC-A1B1C1�У�����A1ACC1�͵���ABC������߳��IJ��ⳤ��Ϊ2��A1B=$\sqrt{6}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��b��c | C�� | a��c��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com