
分析 (1)先把C1的参数方程化为普通方程,再化为极坐标方程;
(2)求出C2的普通方程,与C1的普通方程联立解出交点的直角坐标,转化为极坐标.
解答 解:(1)曲线C1的普通方程为x2+(y-1)2=1,即x2+y2-2y=0,
∴曲线C1的极坐标方程为ρ2-2ρsinθ=0,即ρ=2sinθ.
(2)曲线C2的普通方程为x=-$\frac{\sqrt{3}}{2}$.
把x=-$\frac{\sqrt{3}}{2}$代入x2+y2-2y=0得y=$\frac{1}{2}$或y=$\frac{3}{2}$.
∴曲线C1与曲线C2的交点的直角坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
∴曲线C1与曲线C2的交点的极坐标为(1,$\frac{5π}{6}$),($\sqrt{3}$,$\frac{2π}{3}$).
点评 本题考查了极坐标方程,参数方程与普通方程的转化,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(理)试卷(解析版) 题型:解答题
如图所示,在直三棱柱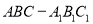 中,平面
中,平面 侧面
侧面 ,且
,且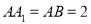 .
.

(1)求证: ;
;
(2)若直线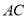 与平面
与平面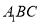 所成角的正弦值为
所成角的正弦值为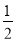 ,求锐二面角
,求锐二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{1+\sqrt{13}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩(∁UN)=∅ | B. | M∩N=N | C. | M∪N=U | D. | M⊆(∁UN) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com