
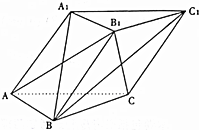
 如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.
如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.分析 ( I)取AC的中点O,A1O,BO.推出BO⊥AC.证明BO⊥侧面ACC1A,得到BO⊥A1O.然后证明A1B⊥AC.A1B⊥AB1,即可证明A1B⊥平面AB1C.
( II)以O为原点,建立如图所示的坐标系,求出相关点的坐标,求出平面ABB1A1的一个法向量,设BC1与平面ABB1A1所成的角为θ,利用向量的数量积求解即可.
解答 ( I)证明:取AC的中点O,A1O,BO.因为△ABC是等边三角形,所以BO⊥AC.…(1分)
因为侧面A1ACC1⊥底面ABC,侧面A1ACC1∩底面ABC=AC,BO⊥AC,
所以BO⊥侧面ACC1A.A1O?侧面ACC1A,∴BO⊥A1O.…(2分)
在Rt△A1BO中,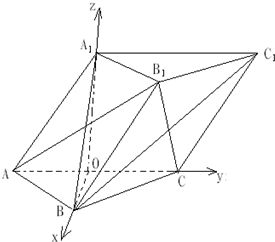
因为${A_1}B=\sqrt{6},BO=\sqrt{3}$,所以${A_1}O=\sqrt{3}$.AA1=2,AO=1,所以${A_1}{O^2}+A{O^2}=A{A_1}^2$.
所以△A1AO为直角三角形,所以A1O⊥AC.…(3分)
又BO⊥AC,A1O∩BO=O,所以AC⊥平面A1BO.A1B?平面A1BO,所以A1B⊥AC.…(4分)
因为四边形ABB1A1为菱形,所以A1B⊥AB1.…(5分)
因为 A1B∩AC=A,所以A1B⊥平面AB1C.…(6分)
( II)解:由( I)知,可以O为原点,建立如图所示的坐标系,由题设条件知,$B(\sqrt{3,}0,0),A(0,-1,0),A_1^{\;}(0,0,\sqrt{3}),{C_1}(0,2,\sqrt{3})$.
所以$\overrightarrow{A{A_1}}=(0,1,\sqrt{3}),\overrightarrow{AB}=(\sqrt{3},1,0),\overrightarrow{B{C_1}}=(-\sqrt{3},2,\sqrt{3})$.…(8分)
设平面ABB1A1的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{A{A}_{1}}=0}\\{\overrightarrow{n}•\overrightarrow{AB}=0}\end{array}\right.$所以$\left\{\begin{array}{l}y+\sqrt{3}z=0\\ \sqrt{3}x+y=0.\end{array}\right.$解得$\left\{\begin{array}{l}x=z\\ y=-\sqrt{3}z.\end{array}\right.$
令z=1,则$\overrightarrow{n}=(1,-\sqrt{3},1)$.…(10分)
设BC1与平面ABB1A1所成的角为θ,
则$sinθ=cos<\overrightarrow{n},\overrightarrow{B{C}_{1}}>=|\frac{\overrightarrow{n}•\overrightarrow{B{C}_{1}}}{|\overrightarrow{n}||\overrightarrow{B{C}_{1}}|}|$=|$\frac{-\sqrt{3}-2\sqrt{3}+\sqrt{3}}{\sqrt{5}×\sqrt{10}}$|=$\frac{\sqrt{6}}{5}$…(12分)
点评 本题考查直线与平面垂直的判定定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(理)试卷(解析版) 题型:选择题
已知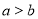 ,二次三项式
,二次三项式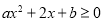 对于一切实数
对于一切实数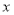 恒成立,又
恒成立,又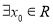 ,使
,使 成立,则
成立,则 的最小值为( )
的最小值为( )
A.1 B. C.2 D.
C.2 D.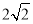
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com