
分析 (1)由2bsinA=$\sqrt{3}$a,利用正弦定理可得:2sinBsinA=$\sqrt{3}$sinA,sinA≠0,化简整理即可得出.
(2)由余弦定理可得:b2=a2+c2-2accosB,代入化简解出即可.
解答 解:(1)在锐角△ABC中,∵2bsinA=$\sqrt{3}$a,∴2sinBsinA=$\sqrt{3}$sinA,sinA≠0,∴sinB=$\frac{\sqrt{3}}{2}$,B∈(0,$\frac{π}{2}$),
∴B=$\frac{π}{3}$.
(2)由余弦定理可得:b2=a2+c2-2accosB,
∴7=(a+c)2-2ac-2accos$\frac{π}{3}$,化为:ac=6,
与a+c=5,a>c,联立解得:a=3,c=2.
点评 本题考查了正弦定理余弦定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(理)试卷(解析版) 题型:解答题
已知 ,二次函数
,二次函数 ,关于
,关于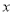 的不等式
的不等式 的解集为
的解集为 ,其中
,其中 为非零常数,设
为非零常数,设 .
.
(1)求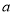 的值;
的值;
(2)若存在一条与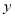 轴垂直的直线和函数
轴垂直的直线和函数 的图象相切,且切点的横坐标
的图象相切,且切点的横坐标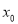 满足
满足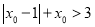 ,求实数
,求实数 的取值范围;
的取值范围;
(3)当实数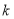 取何值时,函数
取何值时,函数 存在极值?并求出相应的极值点.
存在极值?并求出相应的极值点.
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(文)试卷(解析版) 题型:选择题
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行”的( )
平行”的( )
A. 充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
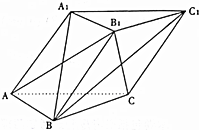 如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.
如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com