
分析 (1)使用二倍角公式用tan$\frac{β}{2}$表示出cosβ,求出$\frac{β}{2}$的范围,解方程得出;
(2)根据α,β的范围求出sinβ,cos(α+β),利用差角的正弦函数公式计算.
解答 解:(1)∵$cosβ={cos^2}\frac{β}{2}-{sin^2}\frac{β}{2}=\frac{{{{cos}^2}\frac{β}{2}-{{sin}^2}\frac{β}{2}}}{{{{cos}^2}\frac{β}{2}+{{sin}^2}\frac{β}{2}}}=\frac{{1-{{tan}^2}\frac{β}{2}}}{{1+{{tan}^2}\frac{β}{2}}}$,且$cosβ=-\frac{1}{3}$,
∴$\frac{{1-{{tan}^2}\frac{β}{2}}}{{1+{{tan}^2}\frac{β}{2}}}=-\frac{1}{3}$,解得${tan^2}\frac{β}{2}=2$,
∵$β∈({\;\frac{π}{2},\;\;π})$,∴$\frac{β}{2}∈({\;\frac{π}{4},\;\;\frac{π}{2}})$,
∴$tan\frac{β}{2}>0$,
∴$tan\frac{β}{2}=\sqrt{2}$.
(2)∵$β∈({\;\frac{π}{2},\;\;π})$,$cosβ=-\frac{1}{3}$,
∴$sinβ=\sqrt{1-{{cos}^2}β}=\sqrt{1-{{({-\frac{1}{3}})}^2}}=\frac{{2\sqrt{2}}}{3}$,
又$α∈({0\;,\;\;\frac{π}{2}})$,故$α+β∈({\frac{π}{2}\;,\;\;\frac{3π}{2}})$,
∴$cos({α+β})=-\sqrt{1-{{sin}^2}({α+β})}=-\sqrt{1-{{({\frac{7}{9}})}^2}}=-\frac{{4\sqrt{2}}}{9}$,
∴sinα=sin[(α+β)-β]=sin(α+β)cosβ-cos(α+β)sinβ=$\frac{7}{9}×({-\frac{1}{3}})$$-({-\frac{{4\sqrt{2}}}{9}})×\frac{{2\sqrt{2}}}{3}=\frac{1}{3}$.
点评 本题考查了三角函数的恒等变换和化简求值,属于中档题.


科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:选择题
已知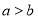 ,二次三项式
,二次三项式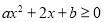 对于一切实数
对于一切实数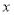 恒成立,又
恒成立,又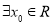 ,使
,使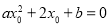 成立,则
成立,则 的最小值为( )
的最小值为( )
A.1 B.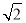 C.2 D.
C.2 D.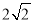
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$-$\frac{\sqrt{3}}{4}$i | B. | $\frac{3}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{3}{4}$+$\frac{\sqrt{3}}{4}$i | D. | $\frac{3}{2}$+$\frac{\sqrt{3}}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com