
分析 根据向量的夹角公式即可求出答案.
解答 解:向量$\overrightarrow{a}$=(2,2,-1),$\overrightarrow{b}$=(3,λ,4),
∴$\overrightarrow{a}•\overrightarrow{b}$=2×3+2λ-1×4=2+2λ,|$\overrightarrow{a}$|=$\sqrt{{2}^{2}+{2}^{2}+(-1)^{2}}$=3,|$\overrightarrow{b}$|=$\sqrt{{3}^{2}+{λ}^{2}+{4}^{2}}$=$\sqrt{25+{λ}^{2}}$,
∵$\overrightarrow{a}$、$\overrightarrow{b}$的夹角的余弦值为$\frac{2}{15}$,
∴$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|\overrightarrow{b}|}$=$\frac{2+2λ}{3•\sqrt{25+{λ}^{2}}}$=$\frac{2}{15}$,
解得λ=0,
故答案为:0.
点评 考查空间向量的数量积和模的运算,和利用数量积求向量的夹角,属基础题.


科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(理)试卷(解析版) 题型:选择题
等比数列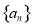 的前
的前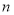 项和为
项和为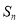 ,已知
,已知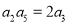 ,且
,且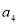 与
与 的等差中项为
的等差中项为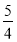 ,则
,则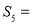 ( )
( )
A.29 B.31 C.33 D.36
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
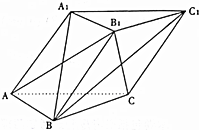 如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.
如图,已知三棱柱ABC-A1B1C1中,侧面A1ACC1⊥底面ABC,底面边长的侧棱长均为2,A1B=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com