
甲、乙两人一起去游玩,他们约定各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后1小时他们在同一个景点的概率是( )
A. B.
B. C.
C.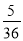 D.
D.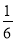
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:填空题
某篮球决赛在广东队与山东队之间进行,比赛采用7局4胜制,即若有一队先胜4场,则此队获胜,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为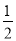 .据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-6几何概型(解析版) 题型:选择题
如图所示,正方形的四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),曲线y=x2经过点B,现将一个质点随机投入正方形中,则质点落在图中阴影区域的概率是( )
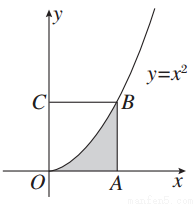
A.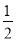 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:选择题
如图所示方格,在每一个方格中填入一个数字,数字可以是1,2,3,4中的任何一个,允许重复.则填入A方格的数字大于B方格的数字的概率为( )
A |
|
| B |
A.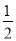 B.
B.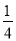 C.
C.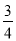 D.
D.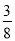
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:解答题
已知(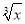 +x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x-
+x2)2n的展开式的二项式系数和比(3x-1)n的展开式的二项式系数和大992,求(2x- )2n的展开式中:
)2n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:填空题
(2x+ )n的展开式中各项系数之和为729,则该展开式中x2的系数为________.
)n的展开式中各项系数之和为729,则该展开式中x2的系数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:填空题
某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排,其中甲、乙两种必须排在一起,而丙、丁两种不能排在一起,不同的排法共有________种.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
已知[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.2]=-2.x0是函数f(x)=ln x- 的零点,则[x0]等于________.
的零点,则[x0]等于________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com