某篮球决赛在广东队与山东队之间进行，比赛采用7局4胜制，即若有一队先胜4场，则此队获胜，比赛就此结束．因两队实力相当，每场比赛两队获胜的可能性均为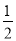
．据以往资料统计，第一场比赛组织者可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元，则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________．
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-11导数的应用一（解析版） 题型：解答题
已知函数f(x)＝(x2＋ax－2a2＋3a)ex(x∈R)，其中a∈R.
(1)当a＝0时，求曲线y＝f(x)在点(1，f(1))处的切线的斜率；
(2)当a≠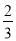
时，求函数y＝f(x)的单调区间与极值．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-10导数的概念及运算（解析版） 题型：解答题
已知函数f(x)＝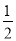
x2－alnx(a∈R)．
(1)若函数f(x)的图象在x＝2处的切线方程为y＝x＋b，求a，b的值；
(2)若函数f(x)在(1，＋∞)上为增函数，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-10导数的概念及运算（解析版） 题型：选择题
设曲线y＝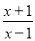
在点(3,2)处的切线与直线ax＋y＋3＝0垂直，则a＝( )
A．2 B．－2 C．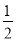
D．－
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：10-8n次独立重复实验与二项分布（解析版） 题型：填空题
已知数列{an}是单调递增的等差数列，从a1，a2，a3，a4，a5，a6，a7中取走任意三项，则剩下四项依然构成单调递增的等差数列的概率是________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：10-8n次独立重复实验与二项分布（解析版） 题型：选择题
甲、乙独立地解决同一数学问题，甲解决这个问题的概率是0．8，乙解决这个问题的概率是0．6，那么其中至少有1人解决这个问题的概率是( )
A．0．48 B．0．52 C．0．8 D．0．92
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：10-6几何概型（解析版） 题型：填空题
在区间[－6,6]内任取一个元素x0，抛物线x2＝4y在x＝x0处的切线的倾斜角为α，则α∈[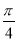
，
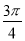]的概率为________．
查看答案和解析>>
科目：高中数学 来源：2015高考数学（理）一轮配套特训：10-4随机事件的概率（解析版） 题型：选择题
甲、乙两人一起去游玩，他们约定各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后1小时他们在同一个景点的概率是( )
A.
B.
C.
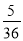D.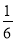
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
＝
．由Sn≥390得n2＋7n≥78，∴n≥6．∴若要获得的门票收入不少于390万元，则至少要比赛6场．①若比赛共进行了6场，则前5场比赛的比分必为2∶3，且第6场比赛为领先一场的球队获胜，其概率P(6)＝
×(
)5＝
；②若比赛共进行了7场，则前6场胜负为3∶3，其概率P(7)＝
×(
)6＝
．∴门票收入不少于390万元的概率P＝P(6)＋P(7)＝
＝
．
在(－2，＋∞)上为增函数，则a的取值范围是________．