
已知函数f(x)=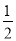 x2-alnx(a∈R).
x2-alnx(a∈R).
(1)若函数f(x)的图象在x=2处的切线方程为y=x+b,求a,b的值;
(2)若函数f(x)在(1,+∞)上为增函数,求a的取值范围.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:选择题
设偶函数f(x)对任意x∈R都有f(x+3)=- ,且当x∈[-3,-2]时,f(x)=4x,则f(107.5)=( )
,且当x∈[-3,-2]时,f(x)=4x,则f(107.5)=( )
A.10 B.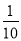 C.-10 D.-
C.-10 D.-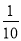
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:填空题
设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:填空题
若函数f(x)=x3-3x+a有三个不同的零点,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:解答题
已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线的方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
(3)如果曲线y=f(x)的某一切线与直线y=- x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:选择题
定义在R上的函数f(x)的导函数为f′(x),已知f(x+1)是偶函数,(x-1)f′(x)<0.若x1<x2,且x1+x2>2,则f(x1)与f(x2)的大小关系是( )
A.f(x1)<f(x2) B.f(x1)=f(x2)
C.f(x1)>f(x2) D.不确定
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:填空题
某篮球决赛在广东队与山东队之间进行,比赛采用7局4胜制,即若有一队先胜4场,则此队获胜,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为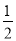 .据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
.据以往资料统计,第一场比赛组织者可获得门票收入40万元,以后每场比赛门票收入比上一场增加10万元,则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功.已知在6道被选题中,甲能答对其中的4道题,乙答对每道题的概率都是.
(1)求甲、乙至少有一人闯关成功的概率;
(2)设甲答对题目的个数为ξ,求ξ的分布列.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:选择题
如图所示方格,在每一个方格中填入一个数字,数字可以是1,2,3,4中的任何一个,允许重复.则填入A方格的数字大于B方格的数字的概率为( )
A |
|
| B |
A.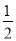 B.
B.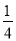 C.
C.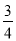 D.
D.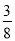
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com