
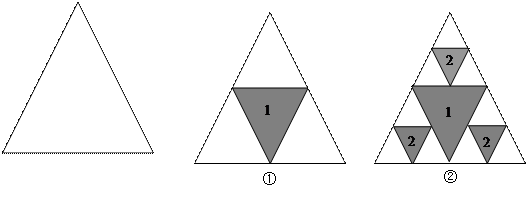
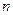 次操作后剩余图形的总面积为
次操作后剩余图形的总面积为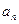
|
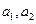 ;(2)求第
;(2)求第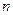 次操作后,挖去的所有三角形上所贴标签上的数字和
次操作后,挖去的所有三角形上所贴标签上的数字和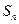 ;
; 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
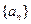 ,规定数列
,规定数列 为数列
为数列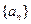 的一阶差分数列,其中
的一阶差分数列,其中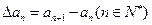 ;一般地,规定
;一般地,规定 为
为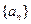 的k阶差分数列,其中
的k阶差分数列,其中 ,且
,且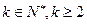 .(I)已知数列
.(I)已知数列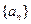 的通项公式
的通项公式 。试证明
。试证明 是等差数列;(II)若数列
是等差数列;(II)若数列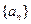 的首项
的首项 ,且满足
,且满足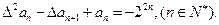 ,求数列
,求数列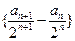 及
及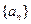 的通项公式;
的通项公式;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
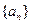 中,
中,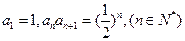 .
. (
(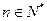 )均为等比数列;??(Ⅱ)求数列
)均为等比数列;??(Ⅱ)求数列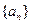 的前
的前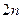 项和
项和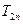 ;???(Ⅲ)若数列
;???(Ⅲ)若数列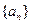 的前
的前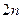 项和为
项和为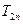 ,不等式
,不等式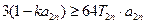 对
对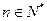 恒成立,求
恒成立,求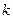 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
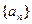 的通项公式为
的通项公式为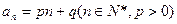 。数列
。数列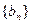 定义如下:对于正整数m,
定义如下:对于正整数m,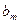 是使得不等式
是使得不等式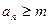 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若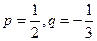 ,求b3; (2)若
,求b3; (2)若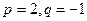 ,求数列
,求数列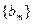 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得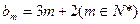 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com