
【题目】如图为某大江的一段支流,岸线![]() 与
与![]() 近似满足
近似满足![]() ∥
∥![]() ,宽度为
,宽度为![]() .圆
.圆![]() 为江中的一个半径为
为江中的一个半径为![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() ,
,![]() .现计划建造一条自小镇
.现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的水上通道
的水上通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切.设
相切.设![]() .
.
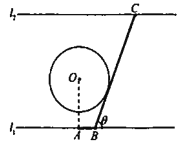
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出定义域;
的函数,并指出定义域;
(2)若建造通道的费用是每公里100万元,则建造此通道最少需要多少万元?
 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() ,已知
,已知![]() .
.
(1)证明:![]() .
.
(2)已知直线![]() 的倾斜角为
的倾斜角为![]() ,设
,设![]() 为椭圆
为椭圆![]() 上不同于
上不同于![]() ,
,![]() 的一点,
的一点,![]() 为坐标原点,线段
为坐标原点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 点,过
点,过![]() 且垂直于
且垂直于![]() 的直线交
的直线交![]() 轴于
轴于![]() 点,若
点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 在第一象限的交点为
在第一象限的交点为![]() ,椭圆
,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其中
,其中![]() 也是抛物线
也是抛物线![]() 的焦点,且
的焦点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左顶点,直线
的左顶点,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
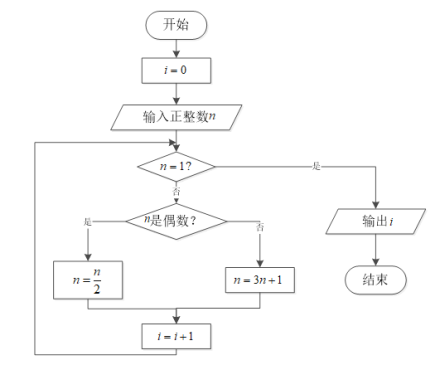
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com