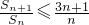证明:由已知,得S
n=3
n-1
要证明
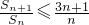
等价于
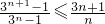
即3
n≥2n+1(*)
(方法一)用数学归纳法证明
①当n=1时,左边=3,右边=3,所以(*)式成立
②假设当n=k时(*)成立,即3
k≥2k+1
那么当n=k+1时,3
k+1=3×3
k≥3(2k+1)=6k+3≥2k+3=2(k+1)+1
所以当n=k+1时(*)也成立
综合①②可得,3
n≥2n+1
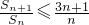
(法二)当n=1时,左边=,右边=4,所以(*)成立
当n≥2时,3
n=(1+2)
n=C
n0+2C
n1+2
2C
n2+…+2
nC
nn=1+2n+…>1+2n
所以
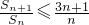
分析:利用等比数列的求和公式可得,S
n=3
n-1,要证明
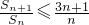
,等价于
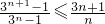
即证3
n≥2n+1(*)成立
(法一)用数学归纳法证明
先验证①当n=1时,(*)式成立,②再假设当n=k时(*)成立,证明当n=k+1时,命题也成立.
(法二)利用二项式定理,检验当n=1时(*)成立
当n≥2时,3
n=(1+2)
n=C
n0+2C
n1+2
2C
n2+…+2
nC
nn=1+2n+…>1+2n
从而可得
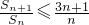
点评:本题主要考查了等比数列的前n项和公式,不等式的证明,数学归纳法证明不等式的应用,二项式定理的运用.

 ≤
≤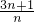 .
.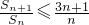 等价于
等价于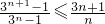 即3n≥2n+1(*)
即3n≥2n+1(*)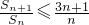
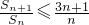
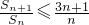 ,等价于
,等价于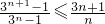 即证3n≥2n+1(*)成立
即证3n≥2n+1(*)成立