Question

【题目】已知椭圆的焦点坐标为F1（﹣1，0），F2（1，0），过F2垂直于长轴的直线交椭圆于P、Q两点，且|PQ|=3．
（1）求椭圆的方程；
（2）过F2的直线l与椭圆交于不同的两点M、N，则△F1MN的内切圆的面积是否存在最大值？若存在求出这个最大值及此时的直线方程；若不存在，请说明理由．

Answer 1

【答案】
（1）解：设椭圆方程为 =1（a＞b＞0），由焦点坐标可得c=1

由|PQ|=3，可得 =3，

又a2﹣b2=1，解得a=2，b= ，

故椭圆方程为 =1

（2）解：设M（x1，y1），N（x2，y2），不妨y1＞0，y2＜0，设△F1MN的内切圆的径R，

则△F1MN的周长=4a=8， （|MN|+|F1M|+|F1N|）R=4R

因此 最大，R就最大，

由题知，直线l的斜率不为零，可设直线l的方程为x=my+1，

由 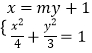得（3m2+4）y2+6my﹣9=0，

得 ， ，

则 = ，

令t= ，则t≥1，

则 ，

令f（t）=3t+ ，则f′（t）=3﹣ ，

当t≥1时，f′（t）≥0，f（t）在[1，+∞）上单调递增，有f（t）≥f（1）=4，S△F1MN≤3，

即当t=1，m=0时，S△F1MN≤3，

S△F1MN=4R，∴Rmax= ，这时所求内切圆面积的最大值为 π．

故直线l：x=1，△F1MN内切圆面积的最大值为 π

【解析】（1）设椭圆方程，由焦点坐标可得c=1，由|PQ|=3，可得 =3，又a2﹣b2=1，由此可求椭圆方程；（2）设M（x1 ， y1），N（x2 ， y2），不妨y1＞0，y2＜0，设△F1MN的内切圆的径R，则△F1MN的周长=4a=8， （|MN|+|F1M|+|F1N|）R=4R，因此 最大，R就最大．设直线l的方程为x=my+1，与椭圆方程联立，从而可表示△F1MN的面积，利用换元法，借助于导数，即可求得结论．
【考点精析】掌握椭圆的标准方程是解答本题的根本，需要知道椭圆标准方程焦点在x轴：，焦点在y轴：．