
【题目】如图所示,M,N,K分别是正方体ABCD—A1B1C1D1的棱AB,CD,C1D1的中点.

求证:(1)AN∥平面A1MK;
(2)平面A1B1C⊥平面A1MK.
【答案】(1)见解析(2)见解析
【解析】试题分析: ![]() 要证明
要证明![]() 平面
平面![]() ,只需要证明
,只需要证明![]() 平行于平面
平行于平面![]() 内的一条直线,容易证明
内的一条直线,容易证明![]() ,从而得到证明;
,从而得到证明;
![]() 要证明
要证明![]() 平面
平面![]() ,只需要证明平面
,只需要证明平面![]() 内的直线
内的直线![]() 垂直于平面
垂直于平面![]() 即可,而
即可,而![]() 容易证明,从而问题得到解决;
容易证明,从而问题得到解决;
解析:证明 (1)如图所示,连接NK.
在正方体ABCD—A1B1C1D1中,
∵四边形AA1D1D,DD1C1C都为正方形,
∴AA1∥DD1,AA1=DD1,C1D1∥CD,C1D1=CD.[2分]
∵N,K分别为CD,C1D1的中点,

∴DN∥D1K,DN=D1K,
∴四边形DD1KN为平行四边形.
∴KN∥DD1,KN=DD1,∴AA1∥KN,AA1=KN.
∴四边形AA1KN为平行四边形.∴AN∥A1K.
∵A1K平面A1MK,AN平面A1MK,
∴AN∥平面A1MK.
(2)如图所示,连接BC1.

在正方体ABCD—A1B1C1D1中,AB∥C1D1,AB=C1D1.
∵M,K分别为AB,C1D1的中点,
∴BM∥C1K,BM=C1K.
∴四边形BC1KM为平行四边形.∴MK∥BC1.
在正方体ABCD—A1B1C1D1中,A1B1⊥平面BB1C1C,
BC1平面BB1C1C,∴A1B1⊥BC1.
∵MK∥BC1,∴A1B1⊥MK.
∵四边形BB1C1C为正方形,∴BC1⊥B1C.
∴MK⊥B1C.
∵A1B1平面A1B1C,B1C平面A1B1C,A1B1∩B1C=B1,∴MK⊥平面A1B1C.
又∵MK平面A1MK,
∴平面A1B1C⊥平面A1MK.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列两圆的位置关系.
(1)C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0;___________
(2)C1:x2+y2-2y=0,C2:x2+y2-2![]() x-6=0;___________
x-6=0;___________
(3)C1:x2+y2-4x-6y+9=0,C2:x2+y2+12x+6y-19=0;___________
(4)C1:x2+y2+2x-2y-2=0,C2:x2+y2-4x-6y-3=0.___________
(5)x2+y2=9和x2+y2-8x+6y+9=0 ________________
(6)圆C1:x2+y2-2x-6y-6=0与圆C2:x2+y2-4x+2y+4=0______
(7)圆x2+y2+6x-7=0和圆x2+y2+6y-27=0 ____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列A: ![]() ,
, ![]() ,…
,… ![]() (N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有
(N≥2)。如果对小于n(2≤n≤N)的每个正整数k都有 ![]() <
< ![]() ,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
,则称n是数列A的一个“G时刻”。记“G(A)是数列A 的所有“G时刻”组成的集合。
(1)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(2)证明:若数列A中存在 ![]() 使得
使得 ![]() >
> ![]() ,则G(A)
,则G(A) ![]()
![]() ;
;
(3)证明:若数列A满足 ![]() -
- ![]() ≤1(n=2,3, …,N),则GA.的元素个数不小于
≤1(n=2,3, …,N),则GA.的元素个数不小于 ![]() -
- ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则![]() 的取值范围是( )
的取值范围是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
(1)A.【选修4—1几何证明选讲】
如图,在△ABC中,∠ABC=90°,BD⊥AC , D为垂足,E是BC的中点,求证:∠EDC=∠ABD.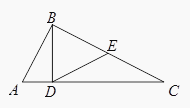
(2)B.【选修4—2:矩阵与变换】
已知矩阵A= ![]() 矩阵B的逆矩阵B﹣1=
矩阵B的逆矩阵B﹣1= 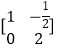 ,求矩阵AB.
,求矩阵AB.
(3)【选修4—4:坐标系与参数方程】在平面直角坐标系xOy中,已知直线l的参数方程为 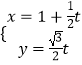 (t为参数),椭圆C的参数方程为
(t为参数),椭圆C的参数方程为 ![]() (
( ![]() 为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
为参数).设直线l与椭圆C相交于A , B两点,求线段AB的长.
(4)D. 设a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求证:|2x+y﹣4|<a.
,求证:|2x+y﹣4|<a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料,生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示:
配料 原料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车品乙种肥料,产生的利润为3万元、分别用x,y表示计划生产甲、乙两种肥料的车皮数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问分别生产甲、乙两种肥料,求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)证明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com