
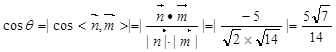 .
. ,
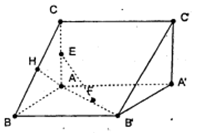
,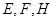 分别是
分别是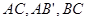 的中点后,可知
的中点后,可知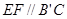 ,这样可以通过证
,这样可以通过证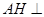 面
面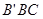 ,得
,得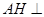
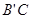 ,故
,故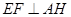 .
.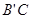 ,
,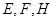 分别是
分别是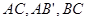 的中点,
的中点,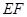 是
是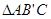 的中位线,
的中位线,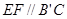 ,………………2分
,………………2分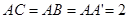 ,
,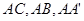 两两垂直知,
两两垂直知,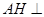
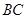 ,又
,又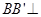 面
面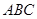 ,
,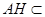 面
面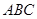 ,则
,则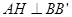 …………4分
…………4分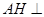 面
面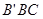 ,则
,则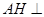
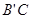 ,故
,故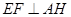 .…………………………6分
.…………………………6分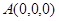
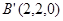
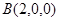
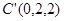
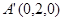
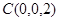
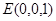
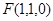
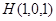
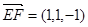 ,
,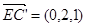
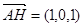
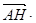
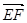 =0,故
=0,故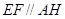
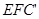 的法向量为
的法向量为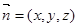 ,
,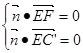 即:
即: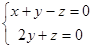 ,
,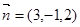 ,………………10分
,………………10分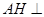 面
面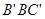 ,不妨令面
,不妨令面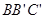 的法向量为
的法向量为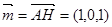
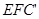 与面
与面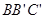 夹角为
夹角为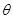 ,
,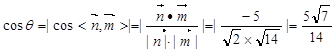


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:不详 题型:单选题
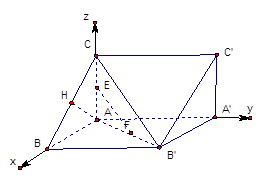
 的棱长为1,线段
的棱长为1,线段 上有两个动点E, F,
上有两个动点E, F, ,
,
A. |
B. |
C.直线 与平面 与平面 所成的角为定值 所成的角为定值 |
D.异面直线 所成的角为定值 所成的角为定值 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 表示两条直线,
表示两条直线, 表示两个平面,现给出下列命题:
表示两个平面,现给出下列命题: ,则
,则 ; ② 若
; ② 若 ,则
,则 ;
; ,则
,则 ; ④ 若
; ④ 若 ,则
,则 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
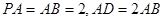 ,PA
,PA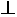 平面ABCD, E,F分别是BC,PC的中点。
平面ABCD, E,F分别是BC,PC的中点。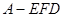 的体积。
的体积。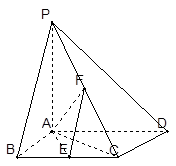
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com