
甲、乙两人下棋,和棋的概率为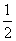 ,乙获胜的概率为
,乙获胜的概率为 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.甲获胜的概率是 B.甲不输的概率是
B.甲不输的概率是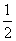
C.乙输了的概率是 D.乙不输的概率是
D.乙不输的概率是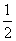
科目:高中数学 来源: 题型:
我们把棱长要么为1 cm,要么为2 cm的三棱锥定义为“和谐棱锥”.在所有结构不同的“和谐棱锥”中任取一个,取到有且仅有一个面是等边三角形的“和谐棱锥”的概率是( )
A.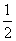 B.
B.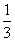
C.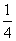 D.
D.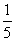
查看答案和解析>>
科目:高中数学 来源: 题型:
若三角形的三边均为正整数,其中一边长为4,另外两边长分别为b、c,且满足b≤4≤c,则这样的三角形有( )
A.10个 B.14个 C.15个 D.21个
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示的几何体是由一个正三棱锥P—ABC与正三棱柱ABC—A1B1C1组合而成,现用3种不同颜色对这个几何体的表面染色(底面A1B1C1不涂色),要求相邻的面均不同色,则不同的染色方案共有________种.
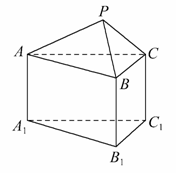
查看答案和解析>>
科目:高中数学 来源: 题型:
现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0、1表示没有击中目标,2、3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了 20组随机数:
7 527 0 293 7 140 9 857 0 347 4 373 8 636 6 947 1 417 4 698 0 371 6 233 2 616 8 045 6 011 3 661 9 597 7 424 7 610 4 281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为 ( )
A.0.852 B.0.819 2 C.0.8 D.0.75
查看答案和解析>>
科目:高中数学 来源: 题型:
一个袋中装有大小相同的黑球、白球和红球.已知袋中共有10个球,从中任意摸出1个球,得到黑球的概率是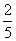 ;从中任意摸出2个球,至少得到1个白球的概率是
;从中任意摸出2个球,至少得到1个白球的概率是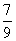 .求:
.求:
(1)从中任意摸出2个球,得到的都是黑球的概率;
(2)袋中白球的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图1,在等腰直角三角形 中,
中, ,
, ,
, 分别是
分别是 上的点,
上的点, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥 ,其中
,其中 .
.
(Ⅰ) 证明: 平面
平面 ; (Ⅱ) 求二面角
; (Ⅱ) 求二面角 的平面角的余弦值.
的平面角的余弦值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com