练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1,在等腰直角三角形中,,,分别是上的点,,为的中点.将沿折起,得到如图2所示的四棱锥,其中.

    (Ⅰ) 证明:平面；      (Ⅱ) 求二面角的平面角的余弦值.


     (Ⅰ) 在图1中,易得

    连结,在中,由余弦定理可得

    由翻折不变性可知,

    所以,所以,

    理可证, 又,所以平面.

    (Ⅱ) 传统法:过作交的延长线于,连结,

    因为平面,所以,

    所以为二面角的平面角.

    结合图1可知,为中点,故,从而

    所以,所以二面角的平面角的余弦值为.

    向量法:以点为原点,建立空间直角坐标系如图所示,

    则,,

    所以,

    设为平面的法向量,则

    ,即,解得,令,得

    由(Ⅰ) 知,为平面的一个法向量,

    所以,即二面角的平面角的余弦值为.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    甲、乙两人下棋，和棋的概率为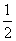，乙获胜的概率为，则下列说法正确的是(　　)

    A．甲获胜的概率是                     B．甲不输的概率是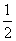

    C．乙输了的概率是                     D．乙不输的概率是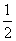

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某企业年初有资金1000万元，如果该企业经过生产经营，每年资金增长率为50%，但每年年底都要扣除消费基金x万元，余下资金投入再生产，为实现经过五年，资金达到2000万元（扣除消费基金后），那么每年扣除的消费资金应是多少万元（精确到万元）。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设为平面内的四点，且

    （1）若求点的坐标；

    （2）设向量若与平行，求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设是两条不同的直线,是两个不同的平面,下列命题中正确的是(    )

    A . 若,,,则  B．若,,,则

    C．若,,,则   D．若,,,则

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图(6)，四棱锥S—ABCD的底面是正方形，侧棱SA⊥底面ABCD，

    过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面

    AEH交SC于K点，且AB=1，SA=2．

    （1）设点P是SA上任一点，试求的最小值；

    （2）求证：E、H在以AK为直径的圆上；

    （3）求平面AEKH与平面ABCD所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在△ABC中，角A，B，C所对的边长分别为a，b，c，若∠C=120°，c=a，则

    A.a＞b            B.a＜b

    C. a＝b            D.a与b的大小关系不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在两个变量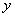与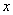的回归模型中，分别选择了4个不同模型，它们的相关指数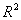如下，其中拟合效果最好的模型是（    ）

    A． 模型1的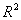为0．55        B．模型2的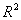为0．65

    C． 模型3的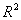为0．79        D．模型4的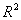为0．95

    查看答案和解析>>

    科目：高中数学 来源： 题型：


        在直角坐标系xOy中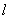，是过定点P(4，2)且倾斜角为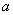的直线；在极坐标系（以坐标原点O为极点，以x轴非负半轴为极轴，取相同单位长度）中，曲线C的极坐标方程为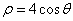

    (I)写出直线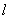的参数方程；并将曲线C的方程化为直角坐标方程；

    ( II)若曲线C与直线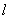相交于不同的两点M、N，求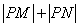的取值范围．

    查看答案和解析>>

    同步练习册答案