Question

15．已知函数f（x）=$\frac{1}{x}$
（1）利用定义法求函数f（x）=$\frac{1}{x}$的导函数
（2）求曲线f（x）=$\frac{1}{x}$过（2，0）的切线方程
（3）求（2）的切线与曲线$f（x）=\frac{1}{x}$及直线x=2所围成的曲边图形的面积．

Answer 1

分析 （1）利用定义法直接求解函数的导数即可．
（2）设出切点坐标，求出曲线的斜率，然后求解切线方程．
（3）利用定积分求解曲边梯形的面积即可．

解答 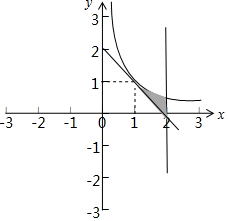解：（1）$△y=\frac{1}{x+△x}-\frac{1}{x}=\frac{-△x}{x（x+△x）}$（1分）
$\frac{△y}{△x}=\frac{-△x}{x（x+△x）△x}=\frac{-1}{x（x+△x）}$（2分）
$f'（x）=\lim_{△x→∞}\frac{△y}{△x}=\lim_{△x→∞}\frac{-1}{x（x+△x）}=-\frac{1}{x^2}$（3分）
（2）设切点P（x₀，y₀），因为$y'=-\frac{1}{x^2}$（4分）
∴$k=-\frac{1}{{{x_0}^2}}$，切线方程$y=-\frac{1}{{{x_0}^2}}（x-2）⇒y=-\frac{1}{{{x_0}^2}}x+\frac{2}{{{x_0}^2}}$
则$\left\{\begin{array}{l}{y_0}=-\frac{1}{{{x_0}^2}}{x_0}+\frac{2}{{{x_0}^2}}\\{y_0}=\frac{1}{x_0}\end{array}\right.$（5分）
$⇒\frac{2}{x_0}=\frac{2}{{{x_0}^2}}⇒{x_0}=1$
所以切线方程y=-x+2（6分）
（3）$\left\{\begin{array}{l}{y=-x+2}\\{y=\frac{1}{x}}\end{array}\right.$，解得x=1，交点坐标（1，1）
$S=\int_1^2{（\frac{1}{x}+x-2）dx}$（7分）
=${∫}_{1}^{2}\frac{1}{x}dx$+${∫}_{1}^{2}xdx$$-2{∫}_{1}^{2}dx$
=$lnx{|}_{1}^{2}$+$\frac{1}{2}{x}^{2}{|}_{1}^{2}$-2x${|}_{1}^{2}$
=ln2-ln1+$\frac{1}{2}（4-1）$-2（2-1）
=ln2-$\frac{1}{2}$（10分）

点评 本题考查函数的导数的应用，切线方程的求法，定积分的应用，考查计算能力．