
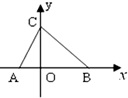
 如图,△ABC中,三个内角B、A、C成等差数列,且AC=20,BC=30.
如图,△ABC中,三个内角B、A、C成等差数列,且AC=20,BC=30.分析 (1)由题意可得:2A=B+C,又A+B+C=180°,可得A=60°.由余弦定理可知:a2=b2+c2-2bccos60°,解出c,可得|AO|,|BO|,即可得出S△ABC.
(2)T=60,可得$ω=\frac{π}{30}$.f(-10)=Msin$[\frac{π}{30}×(-10)+φ]$=0,可得φ.
解答 解:(1)在△ABC中,三个内角B、A、C成等差数列,
∴2A=B+C,又A+B+C=180°,∴A=60°.
由余弦定理可知:a2=b2+c2-2bccos60°,
∴c2-20c-500=0,解得c=10+10$\sqrt{6}$.
又∵|AO|=20cos60°=10,∴|BO|=10$\sqrt{6}$.
∴S△ABC=$\frac{1}{2}×(10+10\sqrt{6})$×$10\sqrt{3}$=50$(3\sqrt{2}+\sqrt{3})$.
(2)T=2×(20+10)=60,
∴$ω=\frac{π}{30}$.
∵f(-10)=Msin$[\frac{π}{30}×(-10)+φ]$=0,
∴sin$(-\frac{π}{3}+φ)$=0,
∴-$\frac{π}{3}$+φ=kπ,k∈Z,|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{3}$.
∵f(0)=Msin$\frac{π}{3}$=10$\sqrt{3}$,解得M=20,
∴f(x)=20sin$(\frac{π}{30}x+\frac{π}{3})$.
点评 本题考查了解三角形、余弦定理、三角函数的图象与性质,考查了推理能力与计算能力,属于中档题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,x2-x≤0”的否定是“?x∈R,x2-x≥0” | |
| B. | “p∧q为真”是“p∨q为真”的必要不充分条件 | |
| C. | “若am2≤bm2,则a≤b”的否命题为真 | |
| D. | ?x∈R,sin2$\frac{x}{2}$+cos2$\frac{x}{2}$=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4α+1>4β+2 | B. | ${log_{\frac{1}{2}}}2α<{log_{\frac{1}{2}}}2β$ | ||
| C. | (α+1)3>β3 | D. | α=β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com