
【题目】已知函数f(x)=x|x﹣2|.
(1)作出函数f(x)=x|x﹣2|的大致图象;
(2)若方程f(x)﹣k=0有三个解,求实数k的取值范围.
(3)若x∈(0,m](m>0),求函数y=f(x)的最大值.
【答案】
(1)解:函数f(x)=x|x﹣2|= 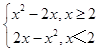 ,
,
由分段函数的画法,可得如图
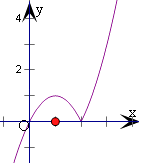
(2)解:若方程f(x)﹣k=0有三个解,即函数f(x)图象与直线y=k有三个交点,
由图可得,当0<k<1时,有三个交点,即方程f(x)﹣k=0有三个解
(3)解:当0<m≤1时,f(x)在(0,m]递增,f(m)取得最大值,且为2m﹣m2;
由x2﹣2x=1,解得x=1+ ![]() (1﹣
(1﹣ ![]() 舍去),
舍去),
当1<m≤1+ ![]() 时,由f(x)的图象可得f(1)取得最大值1;
时,由f(x)的图象可得f(1)取得最大值1;
当m>1+ ![]() 时,由f(x)的图象可得f(m)取得最大值m2﹣2m.
时,由f(x)的图象可得f(m)取得最大值m2﹣2m.
综上可得,当0<m≤1时,f(x)的最大值为2m﹣m2;
当1<m≤1+ ![]() 时,f(x)的最大值为1;
时,f(x)的最大值为1;
当m>1+ ![]() 时,f(x)的最大值为m2﹣2m.
时,f(x)的最大值为m2﹣2m.
【解析】(1)写出f(x)的分段形式,画出图象;(2)由题意可得,函数f(x)图象与直线y=k有三个交点,通过平移直线y=k,即可得到k 范围;(3)对m讨论,分当0<m≤1时,当1<m≤1+ ![]() 时,当m>1+
时,当m>1+ ![]() 时,三种情况,通过图象和单调性,即可得到最大值.
时,三种情况,通过图象和单调性,即可得到最大值.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】若二次函数![]() 的图象和直线
的图象和直线![]() 无交点,现有下列结论:
无交点,现有下列结论:
①方程![]() 一定没有实数根;②若
一定没有实数根;②若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
③若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() ;④若
;④若![]() ,则不等式
,则不等式![]() 对一切实数都成立;⑤函数
对一切实数都成立;⑤函数![]() 的图象与直线
的图象与直线![]() 也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
也一定没有交点,其中正确的结论是__________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的偶函数
上的偶函数![]() ,其导函数为
,其导函数为![]() ,若对任意的实数
,若对任意的实数![]() ,都有
,都有![]() 恒成立,则使
恒成立,则使![]() 成立的实数
成立的实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (b≠0且b是常数).
(b≠0且b是常数).
(1)如果方程f(x)=x有唯一解,求b值.
(2)在(1)的条件下,求证:f(x)在(﹣∞,﹣1)上是增函数;
(3)若函数f(x)在(1,+∞)上是减函数,求负数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列函数:①f(x)=3|x| , ②f(x)=x3 , ③f(x)=ln ![]() ,④f(x)=
,④f(x)= ![]() ,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
,⑤f(x)=﹣x2+1中,既是偶函数,又是在区间(0,+∞)上单调递减函数为 . (写出符合要求的所有函数的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王于年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为(25-x)万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大?(利润=累计收入+销售收入-总支出)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ﹣
﹣ ![]()
(1)证明函数f(x)是奇函数;
(2)证明函数f(x)在(﹣∞,+∞)内是增函数;
(3)求函数f(x)在[1,2]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com