
【题目】如图,在△ABC中,∠B=30°,AC= ![]() ,D是边AB上一点.
,D是边AB上一点.
(1)求△ABC面积的最大值;
(2)若CD=2,△ACD的面积为2,∠ACD为锐角,求BC的长.
【答案】
(1)解:∵ ![]() ,
,
∴由余弦定理可得: 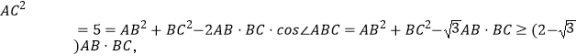
∴ ![]()
∴ ![]() ,
,
所以△ABC的面积的最大值为 ![]()
(2)解:设∠ACD=θ,在△ACD中, ![]() ,
,
∴ ![]() ,解得:
,解得: ![]() ,∴
,∴ ![]()
由余弦定理得: ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,此时
,此时 ![]() ,
,
∴ ![]()
【解析】(1)由已知及余弦定理,基本不等式可得 ![]() ,利用三角形面积公式即可得解△ABC的面积的最大值.(2)设∠ACD=θ,利用三角形面积公式可解得
,利用三角形面积公式即可得解△ABC的面积的最大值.(2)设∠ACD=θ,利用三角形面积公式可解得 ![]() ,可求
,可求 ![]() ,由余弦定理得即可解得AD的值,利用正弦定理可求sinA,进而利用正弦定理可求BC的值.
,由余弦定理得即可解得AD的值,利用正弦定理可求sinA,进而利用正弦定理可求BC的值.
【考点精析】根据题目的已知条件,利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)和动直线l:y=kx+b(k,b是参变量,且k≠0.b≠0)相交于A(x1 , y2),N)x2 , y2)两点,直角坐标系原点为O,记直线OA,OB的斜率分别为kOAkOB= ![]() 恒成立,则当k变化时直线l恒经过的定点为( )
恒成立,则当k变化时直线l恒经过的定点为( )
A.(﹣ ![]() p,0)
p,0)
B.(﹣2 ![]() p,0)
p,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
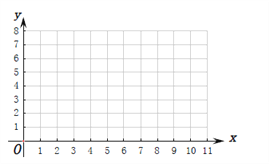
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量x(吨)恰有一个值不超过3(吨)的概率.
参考公式和数据: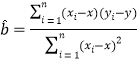 ,
,![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为4的长方形ABCD中,动圆Q的半径为1,圆心Q在线段BC(含端点)上运动,P是圆Q上及内部的动点,设向量 ![]() =m
=m ![]() +n
+n ![]() (m,n为实数),则m+n的取值范围是( )
(m,n为实数),则m+n的取值范围是( ) 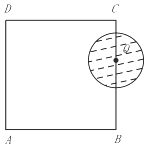
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=8x,圆M:(x﹣2)2+y2=4,点N为抛物线E上的动点,O为坐标原点,线段ON的中点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)点Q(x0 , y0)(x0≥5)是曲线C上的点,过点Q作圆M的两条切线,分别与x轴交于A,B两点,求△QAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x+φ),且 ![]() f(x)dx=0,则下列说法正确的是( )
f(x)dx=0,则下列说法正确的是( )
A.f(x)的一条对称轴为x= ![]()
B.存在φ使得f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
C.f(x)的一个对称中心为( ![]() ,0)
,0)
D.存在φ使得f(x)在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线![]() 上,且经过点A(-3,0),B(1,2).
上,且经过点A(-3,0),B(1,2).
(1)求圆M的方程;
(2)直线![]() 与圆M相切,且
与圆M相切,且![]() 在y轴上的截距是
在y轴上的截距是![]() 在x轴上截距的两倍,求直线
在x轴上截距的两倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com