
【题目】已知函数f(x)=cos(2x+φ),且 ![]() f(x)dx=0,则下列说法正确的是( )
f(x)dx=0,则下列说法正确的是( )
A.f(x)的一条对称轴为x= ![]()
B.存在φ使得f(x)在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
C.f(x)的一个对称中心为( ![]() ,0)
,0)
D.存在φ使得f(x)在区间[ ![]() ,
, ![]() ]上单调递增
]上单调递增
【答案】D
【解析】解:f(x)=cos(2x+φ), ![]() f(x)dx=
f(x)dx= ![]() sin(2x+φ)
sin(2x+φ) ![]() =
= ![]() sin(
sin( ![]() +φ)+
+φ)+ ![]() sinφ=0, ∴tanφ=﹣
sinφ=0, ∴tanφ=﹣ ![]() ,解得φ=﹣
,解得φ=﹣ ![]() +kπ,k∈Z.
+kπ,k∈Z.
令2x﹣ ![]() +kπ=nπ,n∈Z,可得x=
+kπ=nπ,n∈Z,可得x= ![]() (n﹣k)π+
(n﹣k)π+ ![]() ,
,
令 ![]() (n﹣k)π+
(n﹣k)π+ ![]() =
= ![]() π,
π, ![]() =
= ![]() ,矛盾;
,矛盾;
令2mπ≤2x﹣ ![]() +kπ≤π+2mπ,k为奇数,单调减区间为[
+kπ≤π+2mπ,k为奇数,单调减区间为[ ![]() +mπ,
+mπ, ![]() +mπ],不符合题意,k为偶数,单调减区间为[
+mπ],不符合题意,k为偶数,单调减区间为[ ![]() +mπ,
+mπ, ![]() +mπ],不符合题意;
+mπ],不符合题意;
令2x﹣ ![]() +kπ=
+kπ= ![]() π+mπ,x=
π+mπ,x= ![]() +(m﹣k)
+(m﹣k) ![]() =
= ![]() ,∴
,∴ ![]() =
= ![]() ,矛盾;
,矛盾;
令π+2mπ≤2x﹣ ![]() +kπ≤2π+2mπ,k为奇数,单调减区间为[
+kπ≤2π+2mπ,k为奇数,单调减区间为[ ![]() +mπ,
+mπ, ![]() +mπ],符合题意.
+mπ],符合题意.
故选D.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】现有1000根某品种的棉花纤维,从中随机抽取50根,纤维长度(单位:mm)的数据分组及各组的频数如表,据此估计这1000根中纤维长度不小于37.5mm的根数是 .
纤维长度 | 频数 |
[22.5,25.5) | 3 |
[25.5,28.5) | 8 |
[28.5,31.5) | 9 |
[31.5,34.5) | 11 |
[34.5,37.5) | 10 |
[37.5,40.5) | 5 |
[40.5,43.5] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
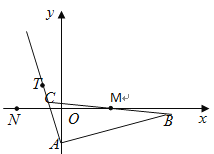
【题目】如图,![]() 的边
的边![]() 边所在直线的方程为
边所在直线的方程为![]()
![]() 满足
满足![]() ,点
,点![]() 在
在![]() 边所在直线上且满足
边所在直线上且满足![]() .
.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求![]() 的外接圆的方程;
的外接圆的方程;
(III)若点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 为正整数。试讨论在
为正整数。试讨论在![]() 的外接圆上是否存在点
的外接圆上是否存在点![]() 使得
使得![]() 成立?说明理由.
成立?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,AC= ![]() ,D是边AB上一点.
,D是边AB上一点.
(1)求△ABC面积的最大值;
(2)若CD=2,△ACD的面积为2,∠ACD为锐角,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据环保部门测定,某处的污染指数与附近污染源的强度成正比,与到污染源距离的平方成反比,比例常数为![]() .现已知相距
.现已知相距![]() 的
的![]() 两家化工厂(污染源)的污染强度分别为
两家化工厂(污染源)的污染强度分别为![]() ,它们连线上任意一点
,它们连线上任意一点![]() 处(异于
处(异于![]() 两点)的污染指数
两点)的污染指数![]() 等于两化工厂对该处的污染指数之和.设
等于两化工厂对该处的污染指数之和.设![]() .
.
(1)试将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,且
,且![]() 时,
时,![]() 取得最小值,试求
取得最小值,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足an>1,其前n项和Sn满足6Sn=an2+3an+2
(1)求数列{an}的通项公式及前n项和Sn;
(2)设数列{bn}满足bn= ![]() ,且其前n项和为Tn , 证明:
,且其前n项和为Tn , 证明: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(0,3),与双曲线
=1(a>b>0)过点A(0,3),与双曲线 ![]() =1有相同的焦点
=1有相同的焦点
(1)求椭圆C的方程;
(2)过A点作两条相互垂直的直线,分别交椭圆C于P,Q两点,则PQ是否过定点?若是,求出定点的坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦晚会期间,高三二班的学生准备了6 个参赛节目,其中有 2 个舞蹈节目,2 个小品节目,2个歌曲节目,要求歌曲节目一定排在首尾,另外2个舞蹈节目一定要排在一起,则这 6 个节目的不同编排种数为
A. 48 B. 36 C. 24 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据a1,a2,…,an的平均数为a,方差为s2,则数据2a1,2a2,…,2an的平均数和方差分别为( )
A. a,s2 B. 2a,s2
C. 2a,2s2 D. 2a,4s2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com