【题目】在如图所示的几何体
中，平面
平面
，四边形
和四边形都是正方形，且边长为
，
是
的中点.
（1）求证：直线
平面
；
（2）求二面角
的大小.
【答案】（1）见解析；（2）
.
【解析】试题分析：（1）连结
交
于
，根据平行四边形性质得是中点，再根据三角形中位线性质得
，最后根据线面平行判定定理得结论,（2）根据条件建立空间直角坐标系,设立各点坐标,利用方程组解各面法向量,根据向量数量积求夹角,最后根据二面角与向量夹角相等或互补关系求二面角.
试题解析：（1）∵且
，
与
交于点
，
与
交于点
∴平面
平面
，∴几何体
是三棱柱
又平面
平面
，
，∴
平面，故几何体是直三棱柱
（1）四边形
和四边形都是正方形，所以
且
，所以四边形
为矩形；于是，连结交于，连结
，是中点，又
是的中点，故是三角形D
的中位线，，注意到在平面
外，在平面内，∴直线
平面
（2）由于平面 
平面，，∴
平面，所以
.于是
，，两两垂直.以
，，所在直线分别为
，
，
轴建立空间直角坐标系，因正方形边长为
，且为中点，所以
，
，
，
于是
，
，设平面
的法向量为
则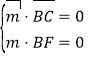
，解之得
，同理可得平面
的法向量
，∴
记二面角
的大小为
，依题意知，为锐角，
，
即求二面角的大小为
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，∠B=30°，AC= 
，D是边AB上一点．
（1）求△ABC面积的最大值；
（2）若CD=2，△ACD的面积为2，∠ACD为锐角，求BC的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】元旦晚会期间，高三二班的学生准备了6 个参赛节目，其中有 2 个舞蹈节目，2 个小品节目，2个歌曲节目，要求歌曲节目一定排在首尾，另外2个舞蹈节目一定要排在一起，则这 6 个节目的不同编排种数为
A. 48 B. 36 C. 24 D. 12
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，椭圆
：
（
）和圆
：
，已知圆将椭圆的长轴三等分，椭圆右焦点到右准线的距离为
，椭圆的下顶点为
，过坐标原点
且与坐标轴不重合的任意直线
与圆相交于点
、
．
（1）求椭圆的方程；
（2）若直线
、
分别与椭圆相交于另一个交点为点
、
.
①求证：直线
经过一定点；
②试问：是否存在以
为圆心，
为半径的圆
，使得直线
和直线
都与圆相交？若存在，请求出实数
的范围；若不存在，请说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着国家二孩政策的全面放开，为了调查一线城市和非一线城市的二孩生育意愿，某机构用简单随机抽样方法从不同地区调查了100位育龄妇女，结果如下表.
非一线城市 | 一线城市 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表：
|
|
|
|
|
|
|
|
|
|
由
算得，
，
参照附表，得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别有关”
B. 在犯错误的概率不超过0.1%的前提下，认为“生育意愿与城市级别无关”
C. 有99%以上的把握认为“生育意愿与城市级别有关”
D. 有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数据a1，a2，…，an的平均数为a，方差为s2，则数据2a1，2a2，…，2an的平均数和方差分别为( )
A. a，s2 B. 2a，s2
C. 2a，2s2 D. 2a，4s2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知sinA+ 
cosA=0，a=2 
，b=2．
（Ⅰ）求c；
（Ⅱ）设D为BC边上一点，且AD⊥AC，求△ABD的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=60°，D是BC上一点，AB=31，BD=20，AD=21．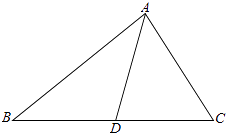 
（1）求cos∠B的值；
（2）求sin∠BAC的值和边BC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
