
 ,第二次出现的点数为
,第二次出现的点数为 ,向量
,向量 ,则向量
,则向量 的概率是 ( )
的概率是 ( )A. | B. | C. | D. |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:填空题
| 分组 | 频数 | 频率 |
| (3.9,4.2] | 3 | 0.06 |
| (4.2,4.5] | 6 | 0.12 |
| (4.5,4.8] | 25 | x |
| (4.8,5.1] | y | z |
| (5.1,5.4] | 2 | 0.04 |
| 合计 | n | 1.00 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
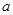 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为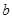 ,其中
,其中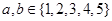 ,若
,若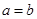 ,或
,或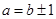 ,就称甲乙“心有灵犀”,现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ▲ .
,就称甲乙“心有灵犀”,现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ▲ .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,第四枪瞄准了三角形
,第四枪瞄准了三角形 射击,第四个弹孔落在三角形
射击,第四个弹孔落在三角形 内
内 ,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).
,求第四个弹孔与前三个弹孔的距离都超过1的概率(忽略弹孔大小).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
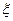 的分布列及数学期望;
的分布列及数学期望;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 “x
“x y为偶数”的概率;
y为偶数”的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 过的信息量为X,当可通过的信息量不小于6时,则可保证校园内的信息通畅.
过的信息量为X,当可通过的信息量不小于6时,则可保证校园内的信息通畅.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y,
,用这两个转盘进行游戏,规则是:同时转动两个转盘待指针停下(当两个转盘中任意一个指针恰好落在分界线时,则这次转动无效,重新开始),记转盘(A)指针所对的区域为x,转盘(B)指针所对的区域为y, ,设
,设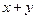 的值为
的值为

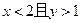 的概率;
的概率;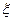 的发布列与数学期望。
的发布列与数学期望。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com