
【题目】某普通高中为了解本校高三年级学生数学学习情况,对一模考试数学成绩进行分析,从中抽取了![]() 名学生的成绩作为样本进行统计(该校全体学生的成绩均在
名学生的成绩作为样本进行统计(该校全体学生的成绩均在![]() ),按下列分组
),按下列分组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 作出频率分布直方图,如图
作出频率分布直方图,如图![]() ;样本中分数在
;样本中分数在![]() 内的所有数据的茎叶图如图
内的所有数据的茎叶图如图![]() :
:

根据往年录取数据划出预录分数线,分数区间与可能被录取院校层次如表.

(1)求![]() 的值及频率分布直方图中的
的值及频率分布直方图中的![]() 值;
值;
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取![]() 人,求此
人,求此![]() 人都不能录取为专科的概率;
人都不能录取为专科的概率;
(3)在选取的样本中,从可能录取为自招和专科两个层次的学生中随机抽取![]() 名学生进行调研,用
名学生进行调研,用![]() 表示所抽取的
表示所抽取的![]() 名学生中为自招的人数,求随机变量
名学生中为自招的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由图![]() 知分数在
知分数在![]() 的学生有
的学生有![]() 名,由图
名,由图![]() 知,频率为
知,频率为![]() ,由此能求出
,由此能求出![]() 的值及频率分布直方图中的
的值及频率分布直方图中的![]() 值;(2)能被专科院校录取的人数为
值;(2)能被专科院校录取的人数为![]() 人,抽取的
人,抽取的![]() 人中,成绩能被专科院校录取的频率是
人中,成绩能被专科院校录取的频率是![]() ,从而从该校高三年级学生中任取
,从而从该校高三年级学生中任取![]() 人能被专科院校录取的概率为
人能被专科院校录取的概率为![]() ,记该校高三年级学生中任取
,记该校高三年级学生中任取![]() 人,都不能被专科院校录取的事件为
人,都不能被专科院校录取的事件为![]() ,由此可求出此
,由此可求出此![]() 人都不能录取为专科的概率;(3)选取的样本中能被专科院校录取的人数为
人都不能录取为专科的概率;(3)选取的样本中能被专科院校录取的人数为![]() 人,成绩能过自招线人数为
人,成绩能过自招线人数为![]() 人,随机变量
人,随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,分别求出随机变量
,分别求出随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
(1)由图![]() 知分数在
知分数在![]() 的学生有
的学生有![]() 名,
名,
又由图![]() 知,频率为:
知,频率为:![]() ,则:
,则:![]()
![]() ,
,![]()
(2)能被专科院校录取的人数为:![]() 人
人
抽取的![]() 人中,成绩能被专科院校录取的频率是:
人中,成绩能被专科院校录取的频率是:![]()
![]() 从该校高三年级学生中任取
从该校高三年级学生中任取![]() 人能被专科院校录取的概率为
人能被专科院校录取的概率为![]()
记该校高三年级学生中任取![]() 人,都不能被专科院校录取的事件为
人,都不能被专科院校录取的事件为![]()
则此![]() 人都不能录取为专科的概率:
人都不能录取为专科的概率: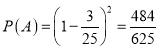
(3)选取的样本中能被专科院校录取的人数为![]() 人
人
成绩能过自招线人数为:![]() 人,
人,
又随机变量![]() 的所有可能取值为
的所有可能取值为![]()
∴![]() ;
;![]() ;
;
![]() ;
;![]()
![]() 随机变量
随机变量![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
![]()


科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.![]() 为曲线
为曲线![]() 右支上的点,点
右支上的点,点![]() 在
在![]() 外角平分线上,且
外角平分线上,且![]() .若
.若![]() 恰为顶角为
恰为顶角为![]() 的等腰三角形,则该双曲线的离心率为( )
的等腰三角形,则该双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为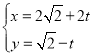 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)把曲线![]() 向下平移
向下平移![]() 个单位,然后各点横坐标变为原来的
个单位,然后各点横坐标变为原来的![]() 倍得到曲线
倍得到曲线![]() (纵坐标不变),设点
(纵坐标不变),设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育部门为研究高中学生的身体素质与课外体育锻炼时间的关系,对该市某校200名高中学生的课外体育锻炼平均每天运动的时间进行调查,数据如下表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间(分钟) |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外体育运动时间在![]() 上的学生评价为“课外体育达标”.
上的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面![]() 列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)从上述课外体育不达标的学生中,按性别用分层抽样的方法抽取10名学生,再从这10名学生中随机抽取3人了解他们锻炼时间偏少的原因,记所抽取的3人中男生的人数为随机变量为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)将上述调查所得到的频率视为概率来估计全市的情况,现在从该市所有高中学生中,抽取4名学生,求其中恰好有2名学生是课外体育达标的概率.
参考公式: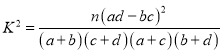 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形![]() ,
,![]() 分别是
分别是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]()
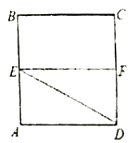
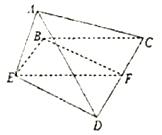
(1)证明:![]()
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的身影
内的身影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com