
【题目】已知正方形![]() ,
,![]() 分别是
分别是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]()
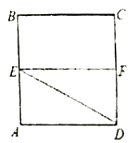
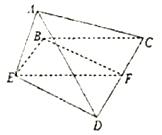
(1)证明:![]()
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的身影
内的身影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的正弦值.
的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)![]() 沿
沿![]() 折起,其它边不变,可知
折起,其它边不变,可知![]() 且
且![]() ,则有四边形
,则有四边形![]() 为平行四边形,那么
为平行四边形,那么![]() ,又由于
,又由于![]() ,
,![]() ,故
,故![]() ;(2)解法一:过点A作
;(2)解法一:过点A作![]() ,垂足为G,连接
,垂足为G,连接![]() ,由于
,由于![]() ,则有
,则有![]() ,故点A在CD的中垂线EF上,过点
,故点A在CD的中垂线EF上,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,由已知得
,由已知得![]() ,故
,故![]() ,则
,则![]() 即是
即是![]() ,设原正方形
,设原正方形![]() 的边长为
的边长为![]() ,根据已知边和角的关系可以求得
,根据已知边和角的关系可以求得![]() ;方法三:点
;方法三:点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上证法同法一,建立空间直角坐标系,先求平面CED的法向量,再求平面ADE的法向量,可得二面角的余弦值,进而得到
上证法同法一,建立空间直角坐标系,先求平面CED的法向量,再求平面ADE的法向量,可得二面角的余弦值,进而得到![]() .
.
解:(1)证明:![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 的中点,
的中点,
∴![]() 且
且![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
又![]() ,而
,而![]() ,
,
∴![]()
(2)解法一:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
∵![]() 为正三角形,
为正三角形,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 垂直平分线上,又∵
垂直平分线上,又∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴点![]() 在平面
在平面 内的射影
内的射影![]() 在直线
在直线![]() 上
上
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]() .
.
设原正方形![]() 的边长为
的边长为![]() ,连接
,连接![]() ,在折后图的
,在折后图的![]() 中,
中,![]() ,
,
∴![]() 为直角三角形,
为直角三角形,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,则
,则![]() ,即
,即![]() .
.
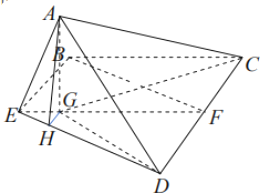
解法二:点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,连接
上,连接![]() ,在平面
,在平面![]() 内过点
内过点![]() 作
作![]() ,垂足为
,垂足为![]()
∵![]() 为正三角形,
为正三角形,![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]()
又∵![]() 且
且![]() ,
,
![]()
∴![]()
∴![]() 为
为![]() 在平面
在平面![]() 内的射影
内的射影![]() ,
,
∴点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上
上
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() ,∴
,∴![]() 是二面角
是二面角![]() 的平面角,即
的平面角,即![]() .
.
设原正方形![]() 的边长为
的边长为![]() ,连接
,连接![]() ,在折后图的
,在折后图的![]() 中,
中,![]() ,
,
∴![]() 为直角三角形,
为直角三角形,![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,则
,则![]() ,即
,即![]() .
.
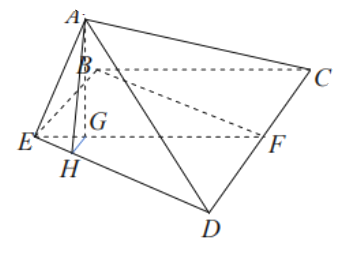
解法三:(同解法一)
点![]() 在平面
在平面![]() 内的射影
内的射影![]() 在直线
在直线![]() 上,
上,
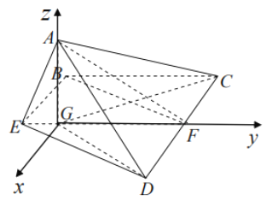
如图,连接![]() ,以
,以![]() 点为坐标原点,
点为坐标原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,过
轴,过![]() 点作平行于
点作平行于![]() 的向量为
的向量为![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
设正方形![]() 的边长为
的边长为![]() ,连接
,连接![]() ,
,![]() .所以
.所以![]() ,
,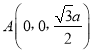 ,
,![]() ,
,![]() ,
,![]() .
.
又平面![]() 的一个法向量为
的一个法向量为![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() .
.
则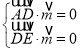 ,即
,即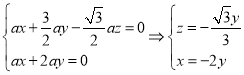 ,所以
,所以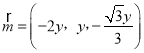
所以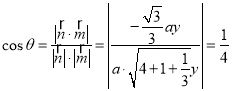 ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】某普通高中为了解本校高三年级学生数学学习情况,对一模考试数学成绩进行分析,从中抽取了![]() 名学生的成绩作为样本进行统计(该校全体学生的成绩均在
名学生的成绩作为样本进行统计(该校全体学生的成绩均在![]() ),按下列分组
),按下列分组![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 作出频率分布直方图,如图
作出频率分布直方图,如图![]() ;样本中分数在
;样本中分数在![]() 内的所有数据的茎叶图如图
内的所有数据的茎叶图如图![]() :
:

根据往年录取数据划出预录分数线,分数区间与可能被录取院校层次如表.

(1)求![]() 的值及频率分布直方图中的
的值及频率分布直方图中的![]() 值;
值;
(2)根据样本估计总体的思想,以事件发生的频率作为概率,若在该校高三年级学生中任取![]() 人,求此
人,求此![]() 人都不能录取为专科的概率;
人都不能录取为专科的概率;
(3)在选取的样本中,从可能录取为自招和专科两个层次的学生中随机抽取![]() 名学生进行调研,用
名学生进行调研,用![]() 表示所抽取的
表示所抽取的![]() 名学生中为自招的人数,求随机变量
名学生中为自招的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成![]() 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
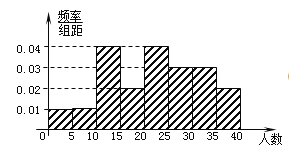
A. 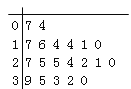 B.
B. 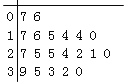
C. 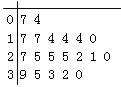 D.
D. 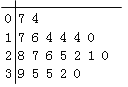
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的准线上一点,F为抛物线的焦点,P为抛物线上的点,且
的准线上一点,F为抛物线的焦点,P为抛物线上的点,且![]() ,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与直线
与直线![]() 的直角坐标方程.
的直角坐标方程.
(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行乒乓球比赛,两人打到![]() 平,之后的比赛要每球交替发球权且要一人净胜两球才能取胜,已知甲发球甲获胜的概率为
平,之后的比赛要每球交替发球权且要一人净胜两球才能取胜,已知甲发球甲获胜的概率为![]() ,乙发球甲获胜的概率为
,乙发球甲获胜的概率为![]() ,则下列命题正确的个数为( )
,则下列命题正确的个数为( )
(1)若![]() ,两人能在两球后结束比赛的概率与
,两人能在两球后结束比赛的概率与![]() 有关
有关
(2)若![]() ,两人能在两球后结束比赛的概率与
,两人能在两球后结束比赛的概率与![]() 有关
有关
(3)第二球分出胜负的概率与在第二球没有分出胜负的情况下进而第四球分出胜负的概率相同
(4)第二球分出胜负的概率与在第![]() 球没有分出胜负的情况下进而第
球没有分出胜负的情况下进而第![]() 球分出胜负的概率相同
球分出胜负的概率相同
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 在
在![]() 轴上,
轴上,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,经过点
,经过点![]() 且垂直于
且垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 到直线
到直线![]() 的最大距离.
的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实常数k和b,使得函数![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 恒成立,则称此直线
恒成立,则称此直线![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() (e为自然对数的底数),有下列命题:
(e为自然对数的底数),有下列命题:
①![]() 内单调递增;
内单调递增;
②![]() 之间存在“隔离直线”,且b的最小值为
之间存在“隔离直线”,且b的最小值为![]() ;
;
③![]() 之间存在“隔离直线”,且k的取值范围是
之间存在“隔离直线”,且k的取值范围是![]() ;
;
④![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的序号为__________.(请填写正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-ABCD中,平面![]() 垂直于对角线AC,且平面
垂直于对角线AC,且平面![]() 截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
截得正方体的六个表面得到截面六边形,记此截面六边形的面积为S,周长为l,则( )
A. S为定值,l不为定值 B. S不为定值,l为定值
C. S与l均为定值 D. S与l均不为定值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com