
【题目】若存在实常数k和b,使得函数![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 恒成立,则称此直线
恒成立,则称此直线![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() (e为自然对数的底数),有下列命题:
(e为自然对数的底数),有下列命题:
①![]() 内单调递增;
内单调递增;
②![]() 之间存在“隔离直线”,且b的最小值为
之间存在“隔离直线”,且b的最小值为![]() ;
;
③![]() 之间存在“隔离直线”,且k的取值范围是
之间存在“隔离直线”,且k的取值范围是![]() ;
;
④![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
其中真命题的序号为__________.(请填写正确命题的序号)
【答案】①②④
【解析】
由题意结合“隔离直线”的定义逐一考查所给的说法是否正确即可.
结合题意逐一考查所给命题的真假:
①∵m(x)=f(x)g(x)=x2![]() ,
,![]() ,则
,则![]() ,
,
∴F(x)=f(x)g(x)在![]() 内单调递增,故①对;
内单调递增,故①对;
②、③设f(x)、g(x)的隔离直线为y=kx+b,则x2kx+b对一切实数x成立,即有△10,k2+4b0,b0,
又![]() kx+b对一切x<0成立,则kx2+bx10,即△20,b2+4k0,k0,
kx+b对一切x<0成立,则kx2+bx10,即△20,b2+4k0,k0,
即有k24b且b24k,k416b264k4k0,同理可得4b0,故②对,③错;
④函数f(x)和h(x)的图象在![]() 处有公共点
处有公共点![]() ,
,
因此若存在f(x)和g(x)的隔离直线,那么该直线过这个公共点,
设隔离直线的斜率为k,则隔离直线方程为ye=k(x![]() ),即y=kxk
),即y=kxk![]() +e,
+e,
由f(x)kxk![]() +e(x∈R),可得x2kx+k
+e(x∈R),可得x2kx+k![]() e0当x∈R恒成立,
e0当x∈R恒成立,
则△0,即![]() ,故
,故![]() ,此时直线方程为:
,此时直线方程为:![]() ,
,
下面证明![]() :
:
令![]() ,则
,则![]() ,
,
当![]() 时,G′(x)=0,当
时,G′(x)=0,当![]() 时,G′(x)<0,当
时,G′(x)<0,当![]() 时,G′(x)>0,
时,G′(x)>0,
则当![]() 时,G(x)取到极小值,极小值是0,也是最小值.
时,G(x)取到极小值,极小值是0,也是最小值.
所以![]() ,则
,则![]() 当x>0时恒成立.
当x>0时恒成立.
∴函数f(x)和g(x)存在唯一的隔离直线![]() ,故④正确.
,故④正确.
故答案为:①②④.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.

(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在已分组的若干数据中,每组的频数是指___________,每组的频率是指____________.
(2)一个公司共有N名员工,下设一些部门,要采用等比例外层随机抽样的方法从全体员工中抽取样本量为n的样本,如果某部门有m名员工,那么从该部门抽取的员工人数是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的非负半轴重合.若曲线
轴的非负半轴重合.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为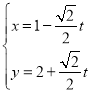 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计后得到如图的频率分布直方图.
,统计后得到如图的频率分布直方图.
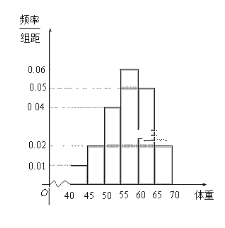
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在![]() 的同学中任意抽取3位,求体重在
的同学中任意抽取3位,求体重在![]() ,
,![]() 内都有同学的概率.
内都有同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆的中心在原点,焦点在坐标轴上,焦距为2![]() .一双曲线和该椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的方程.
.一双曲线和该椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com