
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.
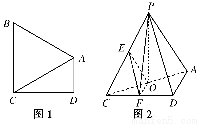
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.
(1)见解析(2)见解析(3)存在
【解析】(1)证明:因为点P在平面ADC上的正投影O恰好落在线段AC上,所以PO⊥平面ADC,所以PO⊥AC.
因为AB=BC,所以O是AC的中点,
所以OE∥PA.
同理OF∥AD.
又OE∩OF=O,PA∩AD=A,
所以平面OEF∥平面PDA.
(2)证明:因为OF∥AD,AD⊥CD,
所以OF⊥CD.
又PO⊥平面ADC,CD?平面ADC,
所以PO⊥CD.
又OF∩PO=O,所以CD⊥平面POF.
(3)存在,事实上记点E为M即可.
因为CD⊥平面POF,PF?平面POF,
所以CD⊥PF.
又E为PC的中点,所以EF=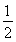 PC,
PC,
同理,在直角三角形POC中,EP=EC=OE=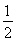 PC,
PC,
所以点E到四个点P,O,C,F的距离相等.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数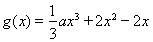 ,函数
,函数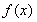 是函数
是函数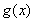 的导函数.
的导函数.
(1)若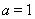 ,求
,求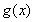 的单调减区间;
的单调减区间;
(2)若对任意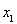 ,
,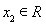 且
且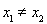 ,都有
,都有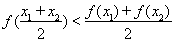 ,求实数
,求实数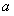 的取值范围;
的取值范围;
(3)在第(2)问求出的实数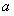 的范围内,若存在一个与
的范围内,若存在一个与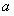 有关的负数
有关的负数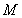 ,使得对任意
,使得对任意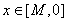 时
时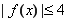 恒成立,求
恒成立,求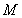 的最小值及相应的
的最小值及相应的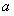 值.
值.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:选择题
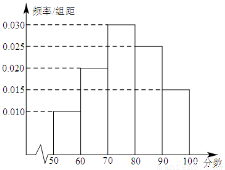
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图,样本数据分组为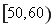 、
、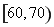 、
、 、
、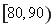 、
、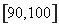 .若用分层抽样的方法从样本中抽取分数在
.若用分层抽样的方法从样本中抽取分数在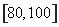 范围内的数据
范围内的数据 个,则其中分数在
个,则其中分数在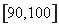 范围内的样本数据有( )
范围内的样本数据有( )
A.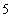 个 B.
个 B.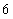 个 C.
个 C.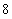 个 D.
个 D.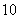 个
个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:填空题
如图是一个空间几何体的三视图,其中正视图和侧视图都是半径为2的半圆,俯视图是半径为2的圆,则该几何体的体积等于________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:选择题
已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′ (x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A.-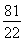 B.
B.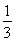 C.2 D.5
C.2 D.5
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷1练习卷(解析版) 题型:选择题
已知双曲线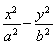 =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
A.|OA|>|OB| B.|OA|<|OB|
C.|OA|=|OB| D.|OA|与|OB|大小关系不确定
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷5练习卷(解析版) 题型:填空题
已知直线l1:ax-y+2a+1=0和l2:2x-(a-1)y+2=0(a∈R),则l1⊥l2的充要条件是a=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com