
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.

根据该折线图,判断下列结论:
(1)月接待游客量逐月增加;
(2)年接待游客量逐年增加;
(3)各年的月接待游客量高峰期大致在7,8月;
(4)各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳.
其中正确结论的个数为( )
A.1B.2C.3D.4
科目:高中数学 来源: 题型:
【题目】定义:若数列![]() 满足所有的项均由
满足所有的项均由![]() ,1构成且其中
,1构成且其中![]() 有
有![]() 个,1有
个,1有![]() 个
个![]() ,则称
,则称![]() 为“
为“![]() 数列”.
数列”.
(1)![]() ,
,![]() ,
,![]() 为“
为“![]() 数列”
数列”![]() 中的任意三项,则使得
中的任意三项,则使得![]() 的取法有多少种?
的取法有多少种?
(2)![]() ,
,![]() ,
,![]() 为“
为“![]() 数列”
数列”![]() 中的任意三项,则存在多少正整数对
中的任意三项,则存在多少正整数对![]() 使得
使得![]() ,且
,且![]() 的概率为
的概率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B为椭圆C:![]() 短轴的上、下顶点,P为直线l:y=2上一动点,连接PA并延长交椭圆于点M,连接PB交椭圆于点N,已知直线MA,MB的斜率之积恒为
短轴的上、下顶点,P为直线l:y=2上一动点,连接PA并延长交椭圆于点M,连接PB交椭圆于点N,已知直线MA,MB的斜率之积恒为![]() .
.

(1)求椭圆C的标准方程;
(2)若直线MN与x轴平行,求直线MN的方程;
(3)求四边形AMBN面积的最大值,并求对应的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某印刷厂为了研究印刷单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表.
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表.
印刷册数 | 2 | 3 | 4 | 5 | 8 |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到了两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
(i)完成下表(计算结果精确到0.1);
印刷册数 | 2 | 3 | 4 | 5 | 8 | |
单册成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
(ii)分别计算模型甲与模型乙的残差平方和![]() 和
和![]() ,并通过比较
,并通过比较![]() ,
,![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷.根据市场调查,新需求量为10千册,若印刷厂以每册5元的价格将书籍出售给订货商,试估计印刷厂二次印刷获得的利润.(按(1)中拟合效果较好的模型计算印刷单册书的成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在北宋1084年第一次印刷出版了《算经十书》,即贾宪的《黄帝九章算法细草》,刘益的《议古根源》,秦九韶的《数书九章》,李冶的《测圆海镜》和《益古演段》,杨辉的《详解九章算法》、《日用算法》和《杨辉算法》,朱世杰的《算学启蒙》和《四元玉鉴》.这些书中涉及的很多方面都达到古代数学的高峰,其中一些“算法”如开立方和开四次方也是当时世界数学的高峰.某图书馆中正好有这十本书现在小明同学从这十本书中任借两本阅读,那么他取到的书的书名中有“算”字的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着城市地铁建设的持续推进,市民的出行也越来越便利.根据大数据统计,某条地铁线路运行时,发车时间间隔t(单位:分钟)满足:4≤t≤15,![]() N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系:
N,平均每趟地铁的载客人数p(t)(单位:人)与发车时间间隔t近似地满足下列函数关系: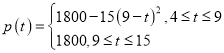 ,其中
,其中![]() .
.
(1)若平均每趟地铁的载客人数不超过1500人,试求发车时间间隔t的值.
(2)若平均每趟地铁每分钟的净收益为![]() (单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
(单位:元),问当发车时间间隔t为多少时,平均每趟地铁每分钟的净收益最大?井求出最大净收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com