练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．6人分别担任六种不同工作，已知甲不能担任第一个工作，则任意分工时，乙没有担任第二项工作的概率为$\frac{21}{25}$．

    分析 先求出甲不能担任第一个工作的种数，再求出甲不能担任第一个工作，乙没有担任第二项工作的种数，根据概率公式计算即可．

    解答 解：甲不能担任第一个工作，有A51A55=600种
    其中甲不能担任第一个工作，乙没有担任第二项工作，
    分两类，第一类：甲担任第二项工作，有A55=120种，
    第一类：甲不担任第二项工作，有C41C41A44=384种，
    故甲不能担任第一个工作，乙没有担任第二项工作的种数为120+384=504，
    故乙没有担任第二项工作的概率为$\frac{504}{600}$=$\frac{21}{25}$，
    故答案为：$\frac{21}{25}$

    点评 本题考查了分类计数原理和古典概率的问题，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    1．若数列{an}是正项数列，且$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+$\sqrt{{a}_{3}}$+…+$\sqrt{{a}_{n}}$=n2+n，则$\frac{1}{{a}_{1}-1}$+$\frac{1}{{a}_{2}-1}$+…+$\frac{1}{{a}_{n}-1}$=$\frac{n}{2n+1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．定义在R上的奇函数f（x）满足f（x-2）=-f（x），且在[0，1]上是增函数，则f（$\frac{1}{4}$），f（-$\frac{1}{4}$），f（$\frac{3}{2}$）的大小关系是$f（-\frac{1}{4}）$＜$f（\frac{1}{4}）$＜$f（\frac{3}{2}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知向量$\overrightarrow{a}$=（sinx，-1），$\overrightarrow{b}$=$（{\sqrt{3}cosx，-\frac{1}{2}}）$．函数f（x）=（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{a}$-2．
    （1）求函数f（x）的单调递减区间；
    （2）已知a，b，c分别为△ABC内角A，B，C 的对边，其中A为锐角，a=2$\sqrt{3}$，c=4，且f（A）=1，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$，$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$，$\sqrt{4+\frac{4}{15}}=4\sqrt{\frac{4}{15}}$，…，$\sqrt{m+\frac{m}{t}}=m\sqrt{\frac{m}{t}}$（m，t∈N*且m≥2），若不等式λm-t-3＜0恒成立，则实数λ的取值范围为（　　）
    A．$[2\sqrt{2}，+∞）$B．$（-∞，2\sqrt{2}）$C．（-∞，3）D．[1，3]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．一个几何体的三视图如图所示，则这个几何体的（　　）
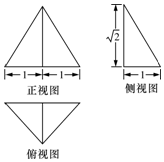
    A．外接球的体积为12$\sqrt{3}$ πB．外接球的表面积为4π
    C．体积为$\sqrt{2}$D．表面积为$\sqrt{5}$+$\sqrt{2}$+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．直线$\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.（{t为参数}）$被圆x2+y2=9截得的弦长为$\sqrt{34}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．某同学同时掷两颗骰子，得到点数分别为a，b，则椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e＞$\frac{{\sqrt{5}}}{3}$的概率是$\frac{5}{18}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知函数f（x）=ax-lnx（a∈R）．
    （Ⅰ）若方程f（x）=0有两根x1，x2，求a的取值范围；
    （Ⅱ）在（Ⅰ）的前提下，设x1＜x2，求证：$\frac{x_2}{x_1}$随着a的减小而增大；
    （Ⅲ）若不等式f（x）≥a恒成立，求证：${（\frac{1}{n}）^n}+{（\frac{2}{n}）^n}+{（\frac{3}{n}）^n}+…+{（\frac{n}{n}）^n}＜a+\frac{1}{{{e}-a}}$（n∈N*）．

    查看答案和解析>>

    同步练习册答案