
���� ��1�����ݺ���f��x��=��$\overrightarrow{a}$+$\overrightarrow{b}$��•$\overrightarrow{a}$-2����������������ɵ�f��x���Ľ���ʽ�������������f��x���ĵ����ݼ����䣮
��2������f��A��=1�������A�Ĵ�С���������Ҷ������b���������ABC�������
��� �⣺��1������$\overrightarrow{a}$=��sinx��-1����$\overrightarrow{b}$=$��{\sqrt{3}cosx��-\frac{1}{2}}��$��
����f��x��=��$\overrightarrow{a}$+$\overrightarrow{b}$��•$\overrightarrow{a}$-2=|$\overrightarrow{a}$|2+$\overrightarrow{a}•\overrightarrow{b}$-2
=sin2x+1+$\sqrt{3}$sinxcosx+$\frac{1}{2}-2$
=$\frac{1}{2}-\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x$-\frac{1}{2}$
=sin��2x-$\frac{��}{6}$����
��$\frac{��}{2}+2k��$2x-$\frac{��}{6}$$��\frac{3��}{2}+2k��$��k��Z��
�ã�$\frac{��}{3}+k��$��x��$\frac{5��}{6}+k��$
���Ժ���f��x���ĵ����ݼ�����Ϊ[$\frac{��}{3}+k��$��$\frac{5��}{6}+k��$]��k��Z��
��2���ɣ�1����֪f��x��=sin��2x-$\frac{��}{6}$��
��ôf��A���Tsin��2A-$\frac{��}{6}$��=1
��$0��A��\frac{��}{2}$��
��$-\frac{��}{6}��$2A-$\frac{��}{6}$$��\frac{5��}{6}$��
��2A-$\frac{��}{6}$=$\frac{��}{2}$��
��A=$\frac{��}{3}$��
�����Ҷ�����a2=b2+c2-2bc•cosA
�ɵã�12=b2+16-4b��
��ã�b=2��
���ABC�����S=$\frac{1}{2}$cbsinA=$4\sqrt{3}$��
���� ���⿼������������������Ǻ����Ļ������������ʵ����ã��Լ����Ҷ����ļ��㣮���ڻ����⣮


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-\frac{{2\sqrt{6}}}{3}��\frac{{2\sqrt{6}}}{3}}��$ | B�� | $��{-\frac{{2\sqrt{3}}}{3}��\frac{{2\sqrt{3}}}{3}}��$ | C�� | $��{-\frac{{\sqrt{3}}}{3}��\frac{{\sqrt{3}}}{3}}��$ | D�� | $��{-\frac{{\sqrt{6}}}{3}��\frac{{\sqrt{6}}}{3}}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$��a��$\frac{3}{2}$ | B�� | $\frac{1}{2}$��a��$\frac{3}{2}$ | C�� | $\frac{1}{2}$��a��$\frac{3}{2}$ | D�� | $\frac{1}{2}$��a��$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
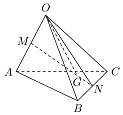 ��ͼ���ռ��ı���OABC�У�M��N�ֱ��ǶԱ�OA��BC���е㣬��G���߶�MN�ϣ���$\overrightarrow{MN}$���ɵĶ���Ϊ2��$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$����x��y��z��ֵ�ֱ�Ϊ$\frac{1}{6}$��$\frac{1}{3}$��$\frac{1}{3}$��
��ͼ���ռ��ı���OABC�У�M��N�ֱ��ǶԱ�OA��BC���е㣬��G���߶�MN�ϣ���$\overrightarrow{MN}$���ɵĶ���Ϊ2��$\overrightarrow{OG}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$����x��y��z��ֵ�ֱ�Ϊ$\frac{1}{6}$��$\frac{1}{3}$��$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
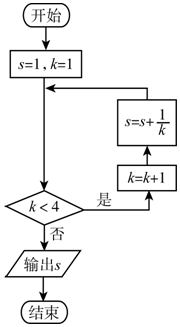
| A�� | $\frac{11}{6}$ | B�� | $\frac{13}{6}$ | C�� | $\frac{25}{12}$ | D�� | $\frac{29}{12}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com