
科目:高中数学 来源: 题型:解答题
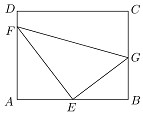 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{3}{4}π,\frac{π}{4}]$ | B. | [-π,0] | C. | $[-\frac{π}{4},\frac{3}{4}π]$ | D. | $[-\frac{π}{2},\frac{π}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{15}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
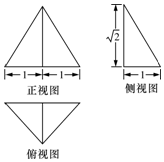
| A. | 外接球的体积为12$\sqrt{3}$ π | B. | 外接球的表面积为4π | ||
| C. | 体积为$\sqrt{2}$ | D. | 表面积为$\sqrt{5}$+$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
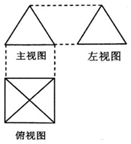 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com