
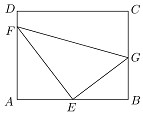
 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.分析 (1)利用三角函数定义表示出EG和FE的长度,利用勾股定理可得长度FG.三边之和可得污水管道的长度l.
(2)根据(1)中的关系式利用三角函数公式化简,利用三角函数的有界限可得l的最大值,即污水净化效果最好.
解答 解:(1)由题意,∠GEB=θ.∠GEF=90°.则∠AEF=90°-θ,
E是AB的中点,AB=20m,$AD=10\sqrt{3}m$,
∴EG=$\frac{10}{cosθ}$,EF=$\frac{10}{cos(90°-θ)}$=$\frac{10}{sinθ}$.
FG=$\sqrt{E{G}^{2}+E{F}^{2}}$=$\frac{10}{cosθsinθ}$
则$l=\frac{10}{sinθ}+\frac{10}{cosθ}+\frac{10}{sinθcosθ}$
定义域:$(θ∈[\frac{π}{6},\frac{π}{3}])$;
(2)由(1)可知则$l=\frac{10}{sinθ}+\frac{10}{cosθ}+\frac{10}{sinθcosθ}$,$(θ∈[\frac{π}{6},\frac{π}{3}])$;
化简可得l=$\frac{10(sinθ+cosθ)+10}{sinθcosθ}$,
令t=sinθ+cosθ=$\sqrt{2}$sin($θ+\frac{π}{4}$).
∵$(θ∈[\frac{π}{6},\frac{π}{3}])$;
∴$θ+\frac{π}{4}$∈[$\frac{5π}{12}$,$\frac{7π}{12}$],
可得sin($θ+\frac{π}{4}$)∈[$\frac{\sqrt{6}+\sqrt{2}}{4}$,1]
则:t∈[$\frac{\sqrt{3}+1}{2}$,$\sqrt{2}$]
可得:sinθcosθ=$\frac{{t}^{2}-1}{2}$,且t≠1.
那么:l=$\frac{10+10t}{\frac{{t}^{2}-1}{2}}$=$\frac{20(1+t)}{{t}^{2}-1}$=$\frac{20}{t-1}$.
当t=$\frac{\sqrt{3}+1}{2}$时,长度l取得最大值为$20\sqrt{3}+20$;
此时:t=$\sqrt{2}$sin($θ+\frac{π}{4}$)=$\frac{\sqrt{3}+1}{2}$,即$θ+\frac{π}{4}$=$\frac{5π}{12}$或$\frac{7π}{12}$
∴$θ=\frac{π}{6}$或$\frac{π}{3}$,
故得$θ=\frac{π}{6}$或$\frac{π}{3}$时,污水净化效果最好,此时管道的长度为$20\sqrt{3}+20$;
点评 本题主要考查对三角函数的应用在实际中的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>c>b | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m≥\frac{1}{e}$ | B. | $0<m≤\frac{1}{e}$ | C. | $m≥\frac{1}{e^2}$ | D. | $0<m≤\frac{1}{e^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com