
| A. | $m≥\frac{1}{e}$ | B. | $0<m≤\frac{1}{e}$ | C. | $m≥\frac{1}{e^2}$ | D. | $0<m≤\frac{1}{e^2}$ |
分析 由题意可得方程$\frac{1}{m}lnx={e}^{mx}$有正根.由y=$\frac{1}{m}lnx$与y=emx互为反函数,则其图象关于直线y=x对称,求其公切点的横坐标,再由$\left\{\begin{array}{l}{\frac{1}{m}lne≥e}\\{{e}^{me}≤e}\end{array}\right.$求得m的范围.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}{e^{mx}}(x≥0)\\ \frac{1}{m}ln(-x)(x<0)\end{array}\right.$的图象上存在关于直线x=0对称的点,
∴函数f(x)=$\frac{1}{m}ln(-x)$(x<0)关于y轴的对称图象与函数f(x)=emx(x≥0)的图象有交点,
即方程$\frac{1}{m}lnx={e}^{mx}$有正根.
∵y=$\frac{1}{m}lnx$与y=emx互为反函数,则其图象关于直线y=x对称,
设y=$\frac{1}{m}lnx$与y=emx的公切点为(x0,x0),
则$\frac{1}{m{x}_{0}}=m{e}^{m{x}_{0}}$,${e}^{m{x}_{0}}=\frac{1}{m}ln{x}_{0}$,联立可得x0=e.
∴$\left\{\begin{array}{l}{\frac{1}{m}lne≥e}\\{{e}^{me}≤e}\end{array}\right.$,解得m$≤\frac{1}{e}$.
又m>0,∴实数m的取值范围是0<m$≤\frac{1}{e}$.
故选:B.
点评 本题考查函数的图象,考查了函数零点的判定,体现了数学转化思想方法,思维难度较大.


科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | 9 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
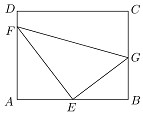 如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.
如图,某污水处理厂要在一个矩形ABCD的池底水平铺设污水净化管道(直角△EFG,E是直角顶点)来处理污水,管道越长,污水净化效果越好,设计要求管道的接口E是AB的中点,F、G分别落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,设∠GEB=θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\frac{3}{4}π,\frac{π}{4}]$ | B. | [-π,0] | C. | $[-\frac{π}{4},\frac{3}{4}π]$ | D. | $[-\frac{π}{2},\frac{π}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
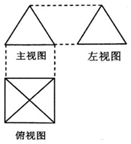 如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.
如图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是$\frac{4\sqrt{3}}{3}$,表面积为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com