
【题目】对于定义域为![]() 的函数
的函数![]() ,部分
,部分![]() 与
与![]() 的对应关系如下表:
的对应关系如下表:
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 2 | 3 | 2 | 0 | -1 | 0 | 2 |
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,且对任意
,且对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图像上,求
的图像上,求![]() ;
;
(3)若![]() ,其中
,其中![]() ,求此函数的解析式,并求
,求此函数的解析式,并求![]() 。
。
【答案】(1)-1;(2)![]() (3)
(3)![]() ,
, ![]()
【解析】
(1)根据复合函数的性质,由内往外计算可得答案.
(2)根据点(xn,xn+1)都在函数y=f(x)的图象上,代入,化简,不难发现函数y是周期函数,即可求解x1+x2+…+x4n的值.
(3)根据表中的数据,由 代入计算即可求解函数的解析式,再利用周期性求得
代入计算即可求解函数的解析式,再利用周期性求得![]() 的值
的值
(1)根据表中的数据:![]() =f(3)=﹣1
=f(3)=﹣1
(2)由题意,x1=2,点(xn,xn+1)都在函数y=f(x)的图象上,
即xn+1=f(xn)
∴x2=f(x1)=f(2)=0,
x3=f(x2)=3,
x4=f(x3)=﹣1,
x5=f(x4)=2
∴x5=x1,
∴函数y是周期为4的函数,由x1+x2+…+x4=4
故得:x1+x2+…+x4n=4n.
(3)由题意得 
∴sin(ω+φ)=sin(﹣ω+φ)∴sinωcosφ=0.
又∵0<ω<π
∴sinω≠0.
∴cosφ=0
而0<φ<π
∴![]()
从而有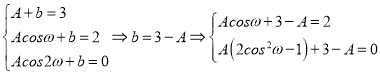 .
.
∴2A2﹣4A+2﹣2A2+3A=0.
∴A=2.b=1![]() ,
,
∵0<ω<π,
∴![]() .
.
∴![]() .
.
此函数的最小正周期T 6,
6,
f(6)=f(0)=3
∵f(1)+f(2)+f(3)+f(4)+f(5)+f(6)=6,
所以![]()


科目:高中数学 来源: 题型:
【题目】如果![]() 项有穷数列
项有穷数列![]() 满足
满足![]() ,即
,即![]() ,那么称有穷数列
,那么称有穷数列![]() 为“对称数列”.例如,由组合数组成的数列
为“对称数列”.例如,由组合数组成的数列![]() 就是“对称数列”.
就是“对称数列”.
(1)设数列![]() 是项数为7的“对称数列”,其中
是项数为7的“对称数列”,其中![]() 成等比数列,且
成等比数列,且![]() 写出数列
写出数列![]() 的每一项;
的每一项;
(2)设数列![]() 是项数为
是项数为![]() 的“对称数列”,其中
的“对称数列”,其中![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() 求
求![]() 取得最大值时
取得最大值时![]() 的取值,并求最大值;
的取值,并求最大值;
(3)设数列![]() 是项数为
是项数为![]() 的对称数列”,且满足
的对称数列”,且满足![]() 记
记![]() 为数列
为数列![]() 的前
的前![]() 项和,若
项和,若![]() 求
求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组测量电视塔AE的高度H(单位m),如示意图,垂直放置的标杆BC高度h=4m,仰角∠ABE=α,∠ADE=β

(1)该小组已经测得一组α、β的值,tanα=1.24,tanβ=1.20,,请据此算出H的值
(2)该小组分析若干测得的数据后,发现适当调整标杆到电视塔的距离d(单位m),使α与β之差较大,可以提高测量精确度,若电视塔实际高度为125m,问d为多少时,α-β最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个墙角,两墙面所成二面角的大小为![]() 有一块长为
有一块长为![]() 米,宽为
米,宽为![]() 米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓
米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓![]() .
.
(1)当![]() 为多少米时,储物仓底面三角形
为多少米时,储物仓底面三角形![]() 面积最大?
面积最大?
(2)当![]() 为多少米时,储物仓的容积最大?
为多少米时,储物仓的容积最大?
(3)求储物仓侧面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:
评分 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频率 | 0.03 | 0.02 | 0.02 | 0.03 | 0.04 | 0.05 | 0.08 | 0.15 | 0.21 | 0.36 |
(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.

(1)求直方图中![]() 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且以
,且以![]() 为直径的圆经过点
为直径的圆经过点![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由.
是否过定点?如果是,请求出该定点;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)写出一个正整数![]() ,使得
,使得![]() 是数列
是数列![]() 的项;
的项;
(3)设数列![]() 的通项公式为
的通项公式为![]() ,问:是否存在正整数
,问:是否存在正整数![]() 和
和![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,请求出所有符合条件的有序整数对
成等差数列?若存在,请求出所有符合条件的有序整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com