
【题目】已知椭圆![]()
![]() ,直线
,直线![]() 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, ![]() 与
与![]() 有两
有两
个交点A、B,线段AB的中点为M.
(1)若![]() ,点K在椭圆
,点K在椭圆![]() 上,
上, ![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
(2)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)若![]() 过点
过点![]() ,射线OM与
,射线OM与![]() 交于点P,四边形
交于点P,四边形![]() 能否为平行四边形?
能否为平行四边形?
若能,求此时![]() 的斜率;若不能,说明理由.
的斜率;若不能,说明理由.
【答案】(1) ![]() (2)见解析(3) 当
(2)见解析(3) 当![]() 的斜率为
的斜率为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形
为平行四边形
【解析】试题分析: ![]() 将
将![]() 代入,求出焦点坐标,设
代入,求出焦点坐标,设![]() ,给出
,给出![]() 的表达式,消元求出范围
的表达式,消元求出范围
![]() 联立直线方程和椭圆方程化简得到
联立直线方程和椭圆方程化简得到![]() ,求出
,求出![]() ,
, ![]() 的值,求出对应的直线斜率即可得到结论
的值,求出对应的直线斜率即可得到结论
![]() 四边形
四边形![]() 为平行四边形,当且仅当线段
为平行四边形,当且仅当线段![]() 与线段
与线段![]() 互相平分,即
互相平分,即![]() ,建立方程关系
,建立方程关系 即可得到结论
即可得到结论
解析:(1)椭圆![]() ,两个焦点
,两个焦点![]() 、
、![]() ,设
,设![]()
所以![]()
由于![]() ,所以
,所以![]() ,
, ![]()
由椭圆性质可知![]() ,所以
,所以![]()
(2)设直线![]() (
(![]() ),
),![]() ,
, ![]() ,
, ![]() ,
,
所以![]() 为方程
为方程![]() 的两根,化简得
的两根,化简得![]() ,
,
所以![]() ,
, ![]() .
.
![]() ,所以直线
,所以直线![]() 的斜率与
的斜率与![]() 的斜率的乘积等于
的斜率的乘积等于![]() 为定值.
为定值.
(3)∵直线![]() 过点
过点![]() ,∴
,∴ ![]() 不过原点且与
不过原点且与![]() 有两个交点的充要条件是
有两个交点的充要条件是![]() ,
, ![]() .
.
设![]() 设直线
设直线![]() (
(![]() ),即
),即![]() .
.
由(2)的结论可知![]() ,代入椭圆方程
,代入椭圆方程![]() 得
得![]()
由(2)的过程得中点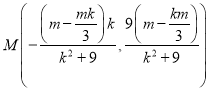 ,
,
若四边形![]() 为平行四边形,那么M也是OP的中点,所以
为平行四边形,那么M也是OP的中点,所以![]() ,
,
得 ,解得
,解得![]()
所以当![]() 的斜率为
的斜率为![]() 或
或![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
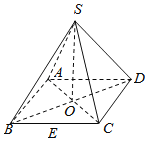
【题目】如图,四棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正方形ABCD,AC与BD的交点为O,
的正方形ABCD,AC与BD的交点为O,![]() 平面ABCD且
平面ABCD且![]() ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持![]() ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 且
且![]() .圆C与直线
.圆C与直线![]() 相切于点A,且点A的纵坐标为
相切于点A,且点A的纵坐标为![]() ,圆心C在直线
,圆心C在直线![]() 上.
上.
(1)求直线![]() 之间的距离;
之间的距离;
(2)求圆C的标准方程;
(3)若直线![]() 经过点
经过点![]() 且与圆C交于
且与圆C交于![]() 两点,当△CPQ的面积最大时,求直线
两点,当△CPQ的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班共有学生45人,其中女生18人,现用分层抽样的方法,从男、女学生中各抽取若干学生进行演讲比赛,有关数据见下表(单位:人)
性别 | 学生人数 | 抽取人数 |
女生 | 18 |
|
男生 |
| 3 |
(1)求![]() 和
和![]() ;
;
(2)若从抽取的学生中再选2人做专题演讲,求这2人都是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来郑州空气污染较为严重,现随机抽取一年(365天)内100天的空气中![]() 指数的监测数据,统计结果如下:
指数的监测数据,统计结果如下:
|
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为![]() .当
.当![]() 在区间
在区间![]() 内时对企业没有造成经济损失;当
内时对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时对企业造成经济损失成直线模型(当
内时对企业造成经济损失成直线模型(当![]() 指数为150时造成的经济损失为500元,当
指数为150时造成的经济损失为500元,当![]() 指数为200时,造成的经济损失为700元);当
指数为200时,造成的经济损失为700元);当![]() 指数大于300时造成的经济损失为2000元.
指数大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于500元且不超过900元的概率;
大于500元且不超过900元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面列联表,并判断是否有![]() 的把握认为郑州市本年度空气重度污染与供暖有关?
的把握认为郑州市本年度空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
![]() ,其中
,其中![]() .
.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家销售公司拟各招聘一名产品推销员,日工资方案如下: 甲公司规定底薪80元,每销售一件产品提成1元; 乙公司规定底薪120元,日销售量不超过45件没有提成,超过45件的部分每件提成8元.
(I)请将两家公司各一名推销员的日工资![]() (单位: 元) 分别表示为日销售件数
(单位: 元) 分别表示为日销售件数![]() 的函数关系式;
的函数关系式;
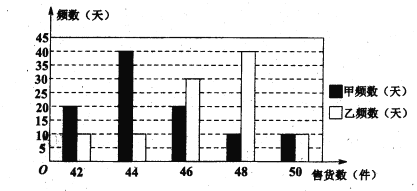
(II)从两家公司各随机选取一名推销员,对他们过去100天的销售情况进行统计,得到如下条形图。若记甲公司该推销员的日工资为![]() ,乙公司该推销员的日工资为
,乙公司该推销员的日工资为![]() (单位: 元),将该频率视为概率,请回答下面问题:
(单位: 元),将该频率视为概率,请回答下面问题:
某大学毕业生拟到两家公司中的一家应聘推销员工作,如果仅从日均收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
【答案】(I)见解析; (Ⅱ)见解析.
【解析】分析:(I)依题意可得甲公司一名推销员的工资与销售件数的关系是一次函数的关系式,而乙公司是分段函数的关系式,由此解得;(Ⅱ)分别根据条形图求得甲、乙公司一名推销员的日工资的分布列,从而可分别求得数学期望,进而可得结论.
详解:(I)由题意得,甲公司一名推销员的日工资![]() (单位:元) 与销售件数
(单位:元) 与销售件数![]() 的关系式为:
的关系式为: ![]() .
.
乙公司一名推销员的日工资![]() (单位: 元) 与销售件数
(单位: 元) 与销售件数![]() 的关系式为:
的关系式为: 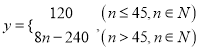
(Ⅱ)记甲公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
记乙公司一名推销员的日工资为![]() (单位: 元),由条形图可得
(单位: 元),由条形图可得![]() 的分布列为
的分布列为
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴仅从日均收入的角度考虑,我会选择去乙公司.
点睛:求解离散型随机变量的数学期望的一般步骤为:
第一步是“判断取值”,即判断随机变量的所有可能取值,以及取每个值所表示的意义;
第二步是“探求概率”,即利用排列组合,枚举法,概率公式,求出随机变量取每个值时的概率;
第三步是“写分布列”,即按规范形式写出分布列,并注意用分布列的性质检验所求的分布列或某事件的概率是否正确;
第四步是“求期望值”,一般利用离散型随机变量的数学期望的定义求期望的值
【题型】解答题
【结束】
19
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
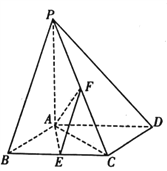
(1)证明: ![]() ;
;
(2)设![]() 为线段
为线段![]() 上的动点,若线段
上的动点,若线段![]() 长的最小值为
长的最小值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)为进一步提高购物者的满意度,平台按分层抽样方法从中抽取![]() 次交易进行问卷调查,详细了解满意与否的具体原因,并在这
次交易进行问卷调查,详细了解满意与否的具体原因,并在这![]() 次交易中再随机抽取
次交易中再随机抽取![]() 次进行电话回访,听取购物者意见.求电话回访的
次进行电话回访,听取购物者意见.求电话回访的![]() 次交易至少有一次对商品和快递都满意的概率.
次交易至少有一次对商品和快递都满意的概率.
附: 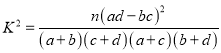 (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P—ABCD的底面是边长为a的棱形,PD⊥底面ABCD.

(1)证明:AC⊥平面PBD;
(2)若PD=AD,直线PB与平面ABCD所成的角为45°,四棱锥P—ABCD的体积为![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com