
分析 使函数y=sinωx在区间[$\frac{π}{4}$,$\frac{π}{3}$]上不单调,只需对称轴在[$\frac{π}{4}$,$\frac{π}{3}$]即可.
解答 解:根据正弦函数图象及性质:
对称轴方程为ωx=$\frac{π}{2}+kπ$,(k∈Z).
解得:x=$\frac{π}{2ω}+\frac{kπ}{ω}$,(k∈Z).
∵函数y=sinωx在区间[$\frac{π}{4}$,$\frac{π}{3}$]上不单调,
∴$\frac{π}{4}$<$\frac{π}{2ω}+\frac{kπ}{ω}$<$\frac{π}{3}$,(k∈Z),
解得:1.5+3k<ω<2+4k,(k∈Z).
由题意:ω∈N*且ω≤15
当k=0时,1.5<ω<2,此时ω没有正整数可取;
当k=1时,4.5<ω<6,此时ω可以取:5;
当k=2时,7.5<ω<10,此时ω可以取:8,9;
当k=3时,10.5<ω<14,此时ω可以取:11,12,13;
当k=4时,13.5<ω<18,此时ω可以取:14,15;
∴ω∈N*且ω≤15,y=sinωx在区间[$\frac{π}{4}$,$\frac{π}{3}$]上不单调时,ω可以4个数,即,5,8,9,11,12,13;14,15.
故答案为:8.
点评 本题考查了正弦函数图象及性质的灵活运用.属于基础题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
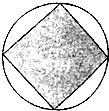 我们知道,可以用模拟的方法估计圆周率p的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为n,落到正方形内的豆子数为m,则圆周率p的估算值是( )
我们知道,可以用模拟的方法估计圆周率p的近似值,如图,在圆内随机撒一把豆子,统计落在其内接正方形中的豆子数目,若豆子总数为n,落到正方形内的豆子数为m,则圆周率p的估算值是( )| A. | $\frac{n}{m}$ | B. | $\frac{2n}{m}$ | C. | $\frac{3n}{m}$ | D. | $\frac{2m}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<p<n | B. | m<n<p | C. | n<m<p | D. | n<p<m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B={-2,-1} | B. | (∁RA)∪B=(-∞,0) | C. | A∪B=(0,+∞) | D. | (∁RA)∩B={-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com