
某市准备从5名报名者(其中男3人,女2人)中选2人参加两个副局长职务竞选。
(1)求所选2人均为女副局长的概率;
(2)若选派两个副局长依次到A、B两个局上任,求A局是男副局长的情况下,B局是女副局长的概率。
科目:高中数学 来源: 题型:解答题
袋中有4个红球,3个黑球,从袋中随机地抽取4个球,设取到1个红球得2分,取到1个黑球得1分.
(1)求得分X的分布列;(2)求得分大于6的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位招聘职工,经过几轮筛选,一轮从2000名报名者中筛选300名进入二轮笔试,接着按笔试成绩择优取100名进入第三轮面试,最后从面试对象中综合考察聘用50名.
(1)求参加笔试的竞聘者能被聘用的概率;
(2)用分层抽样的方式从最终聘用者中抽取10名进行进行调查问卷,其中有3名女职工,求被聘用的女职工的人数;
(3)单位从聘用的三男和二女中,选派两人参加某项培训,至少选派一名女同志参加的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 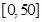 | 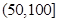 | 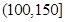 | 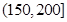 | 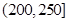 | 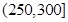 | 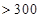 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
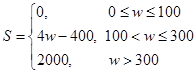 ,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
,试估计在本年度内随机抽取一天,该天经济损失S大于200元且不超过600元的概率; 列联表,并判断能否有
列联表,并判断能否有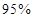 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?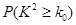 | 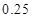 | 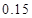 | 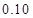 | 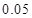 | 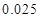 | 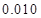 | 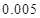 | 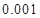 |
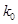 | 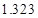 | 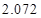 | 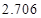 | 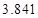 | 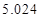 | 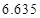 | 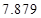 | 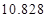 |
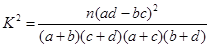
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校举行环保知识大奖赛,比赛分初赛和决赛两部分.初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题连续两次答错的概率为 .(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
.(已知甲回答每个问题的正确率相同,并且相互之间没有影响.)
(1)求选手甲回答一个问题的正确率.
(2)求选手甲可进入决赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋内装有6个球,这些球依次被编号为1、2、3、……、6,设编号为n的球重n2-6n+12(单位:克),这些球等可能地从袋里取出(不受重量、编号的影响).
(1)从袋中任意取出一个球,求其重量大于其编号的概率;
(2)如果不放回地任意取出2个球,求它们重量相等的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有标号分别为1,2,3的三个小球.现从这个盒子中,有放回地先后抽得两个小球的标号分别为x,y,设O为坐标原点,M的坐标为(x-2,x-y).
(1)求|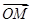 |2的所有取值之和;
|2的所有取值之和;
(2)求事件“|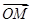 |2取得最大值”的概率.
|2取得最大值”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为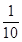 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为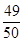 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.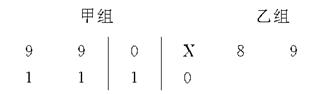
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数Y的分布列和数学期望.(注:方差s2=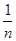 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com