
| ���� | ��ѧ | |||
| ���� | ���� | ���� | ||
| ���� | ���� | 7 | 20 | 5 |
| ���� | 9 | 18 | 6 | |
| ���� | a | 4 | b | |
���� ��1���ɸ������У���ѧ�ɼ���������30%�������a��b��ֵ��
��2���ڵ��P��ѧ���У�a+b=31�����ɡ�a��10��b��7�������оٷ��������ѧ�ɼ�����������ȼ���������ٵĸ��ʣ�
��� ����С������Ϊ12�֣�
�⣺��1���߸������У���ѧ�ɼ���������30%��
��$\frac{7+9+a}{100}=30%$��
���a=14��b=100-30-��20+18+4��-��5+6��=17����5�֣�
��2���ڵ��P��ѧ���У�a+b=100-��7+20+5��-��9+18+6��-4=31����6�֣�
��a��10��b��7����a��b�Ĵ����У�
��10��21������11��20������12��19������13��18������14��17������15��16������16��15����
��17��14������18��13������19��12������20��11������21��10������22��9������23��8����
��24��7����22��9������23��8������24��7��������15�֡���8�֣�
�ǡ���ѧ�ɼ�����������ȼ���������١�Ϊ�¼�A���ɵ�7+9+a��5+6+b����a+5��b��
�¼�A��������10��21������11��20������12��19������3�������¼�������10�֣�
���ԣ���ѧ�ɼ�����������ȼ���������ٵĸ���P��A��=$\frac{3}{15}$=$\frac{1}{5}$������12�֣�
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע��ȿ����¼����ʼ��㹫ʽ���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
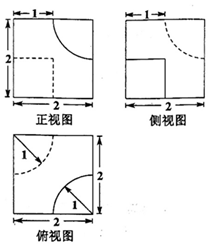 ��ͼ��ʾij���������ͼ���������������Ϊ��������
��ͼ��ʾij���������ͼ���������������Ϊ��������| A�� | $8-\frac{5��}{12}$ | B�� | $8-\frac{��}{3}$ | C�� | $8-\frac{��}{2}$ | D�� | $8-\frac{7��}{12}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{16}$ | C�� | 20 | D�� | 40 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\sqrt{3}$��$\sqrt{3}$�� | B�� | ��-$\sqrt{5}$��$\sqrt{5}$�� | C�� | ��-$\frac{\sqrt{5}}{2}$��$\frac{\sqrt{5}}{2}$�� | D�� | ��-$\frac{\sqrt{3}}{2}$��$\frac{\sqrt{3}}{2}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com