
分析 (Ⅰ)求得切点坐标和函数的导数,可得切线的斜率,运用点斜式方程可得切线的方程;
(II)求导,根据导数与函数单调性及极值的关系,即可求得函数y=f(x)的单调区间和极值.
解答 解:(Ⅰ)由f(x)=xex,f(1)=e,求导f′(x)=ex+xex=(1+x)ex,
∴f′(1)=2e,
∴点P(1,f(1))处的切线方程y-f(1)=f′(1)(x-1),即y-e=2e(x-1),
整理得:y=2ex-e,
曲线y=f(x)在点P(1,f(1))处的切线方程y=2ex-e;
(II)∵函数f(x)=xex的定义域为R,
f'(x)=(xex)′=x′ex+x(ex)′=ex+xex,
令f'(x)=ex+xex=ex(1+x)=0,解得:x=-1.
则x,f′(x),f(x)的变化:
| x | (-∞,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,利用导数求函数的单调性及极值,考查转化思想,属于中档题.


科目:高中数学 来源: 题型:解答题
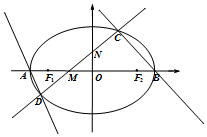 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | (-∞,0)∪{1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com