
【题目】求值
(1)已知f(3x)=xlg9,求f(2)+f(5)的值;
(2)若3a=5b=A(ab≠0),且 ![]() =2,求A的值.
=2,求A的值.
【答案】
(1)解 :由f(3x)=xlg9得f(3x)=2lg3x,于是f(x)=2lgx.
f(2)+f(5)=2lg2+2lg5=2lg10=2
(2)解 :由3a=5b=A(ab≠0),得alg3=blg5=lgA≠0,
于是 ![]() ,
, ![]() .
.
代入 ![]() =2得
=2得 ![]() =2,
=2,
所以lg3+lg5=2lgA,即有A= ![]()
【解析】(1)由已知,运用换元法,求得f(x),再由对数的运算性质,即可得到;(2)运用对数形式求得a,b,再由换底公式得到 ![]() ,再由对数的运算性质,即可得到.
,再由对数的运算性质,即可得到.
【考点精析】利用函数的值和基本不等式对题目进行判断即可得到答案,需要熟知函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法;基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为[5,15],(15,25],(25,35],(35,45],由此得到样本的重量频率分布直方图(如图).
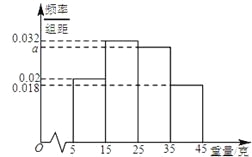
(1)求![]() 的值;
的值;
(2)从盒子中随机抽取3个小球,其中重量在[5,15]内的小球个数为X,求X的分布列和数学期望. (以直方图中的频率作为概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟订的价格进行试销得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 92 | 82 | 83 | 80 | 75 | 68 |
(1)求出y关于x的线性回归方程 ![]() .其中
.其中 ![]() =250
=250
(2)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元每件,为使工厂获得最大利润,该产品的单价应定为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)满足f(x﹣1)=2x+3a,且f(a)=7.
(1)求函数f(x)的解析式;
(2)若g(x)=xf(x)+λf(x)+x在[0,2]上最大值为2,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据以往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为
(升),在水底作业10个单位时间,每单位时间用氧量为0.9(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为
(米/单位时间),每单位时间用氧量为1.5(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)= ![]() 的定义域集合是A,函数g(x)=lg[x2﹣(2a+1)x+a2+a]的定义域集合是B.
的定义域集合是A,函数g(x)=lg[x2﹣(2a+1)x+a2+a]的定义域集合是B.
(1)求集合A,B.
(2)若A∪B=B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com