
【题目】在竖直坐标平面![]() 中,从坐标原点
中,从坐标原点![]() 出发以同一初速度
出发以同一初速度![]() 和不同的发射角(即发射方向与
和不同的发射角(即发射方向与![]() 轴正向之间的夹角)
轴正向之间的夹角)![]() 射出的质点(不计质点的大小),在重力(设重力加速度为
射出的质点(不计质点的大小),在重力(设重力加速度为![]() )的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线
)的作用下运动轨迹是抛物线,所有这些抛物线组成一个抛物线族(即抛物线的集合).若两条抛物线在同一个交点处的切线互相垂直,则称这个交点为正交点.证明:此抛物线族的所有正交点的集合是一段椭圆弧,并求出这个椭圆弧的方程(包括变量的取值范围),再画出它的草图.注. 抛物线![]() 在其上的点
在其上的点![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
【答案】见解析
【解析】
如图,设在时刻![]() 时质点坐标为
时质点坐标为![]() ,
,
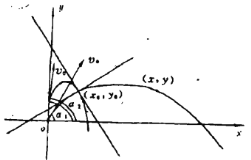
![]() 时质点在坐标原点
时质点在坐标原点![]() .由物理学公式得
.由物理学公式得
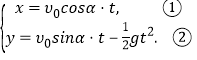
由①得 ![]() ,代入②得
,代入②得
![]() ,
,
亦即 ![]() . ③
. ③
这就是以![]() 为发射角的质点的运动轨迹方程.
为发射角的质点的运动轨迹方程.
另外,由![]() ,知
,知![]() ,
,![]() 与
与![]() 同号.
同号.
由题注知,抛物线③在点![]() 处的切线的斜率为
处的切线的斜率为
![]() .
.
设正交点为![]() ,两条抛物线所对应的发射角分别为
,两条抛物线所对应的发射角分别为![]() 和
和![]() ,则由“正交点”的定义得
,则由“正交点”的定义得
![]()
![]() .
.
又因为![]() 在这两条抛物线上,故
在这两条抛物线上,故
![]() . ⑤
. ⑤
显然原点![]() 是“正交点”,这只须取
是“正交点”,这只须取![]() 即可.故下面设
即可.故下面设![]() .由⑤得
.由⑤得
把上式代入④得
![]() ,
,
即 ![]()
![]() . ⑥
. ⑥
又由⑤知,![]() 和
和![]() 是下列一元二次方程(设
是下列一元二次方程(设![]() 为未知元)
为未知元)
![]() ⑦
⑦
的两个根,故由根与系数的关系得
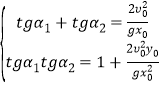 . ⑧
. ⑧
把⑧代入⑥得
![]() ,
,
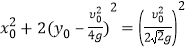 ,
,
即 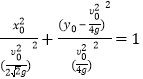 . ⑨
. ⑨
另外,由![]() (因为
(因为![]() )知⑦应有两个不同的实根,从而⑦的判别式应大于零,即
)知⑦应有两个不同的实根,从而⑦的判别式应大于零,即
![]() ,
,
亦即 ![]() . ⑩
. ⑩
又由⑨得 ![]() ,所以,⑩变为
,所以,⑩变为
![]() ,
,
![]() ,
,
即 ![]() .
. ![]()
但由⑨得![]() ,这样由
,这样由![]() 知,只能有
知,只能有
![]() .
. ![]()
综合⑨和![]() 知,所有“正交点“的集合是下列方程所表示的曲线:
知,所有“正交点“的集合是下列方程所表示的曲线:
 .
. ![]()
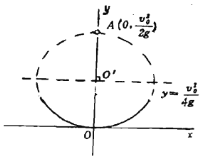
它所表示的曲线如下图所示,即椭圆上除去上顶点![]() 以外,却都可以成为“正交点”.
以外,却都可以成为“正交点”.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
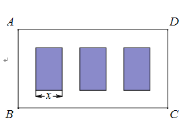
【题目】某广场要划出一块矩形区域![]() ,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设
,在其中开辟三块完全相同的矩形绿化园圃,空白处均铺设![]() 宽的走道,如图.已知三块园圃的总面积为
宽的走道,如图.已知三块园圃的总面积为![]() ,设园圃小矩形的一边长为
,设园圃小矩形的一边长为![]() ,区域
,区域![]() 的面积为
的面积为![]() (单位:
(单位:![]() ).
).
(1)求![]() 的最小值.
的最小值.
(2)若区域![]() 的面积不超过
的面积不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用![]() 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为![]() 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:厘米)满足关系:
(单位:厘米)满足关系:![]() .若不建隔热层,每年的能源消耗费用为
.若不建隔热层,每年的能源消耗费用为![]() 万元.设
万元.设![]() 为隔热层建造费用与
为隔热层建造费用与![]() 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 最小,并求其最小值.
最小,并求其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南充高中扎实推进阳光体育运动,积极引导学生走向操场,走进大自然,参加体育锻炼,每天上午第三节课后全校大课间活动时长35分钟.现为了了解学生的体育锻炼时间,采用简单随机抽样法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下表:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计我校7000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人;
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点, ![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com