练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】（1）已知一元二次方程的两根分别为2和，求关于的不等式的解集.

    （2）求关于的不等式的解集

    【答案】(1) (2)答案不唯一，见解析

    【解析】

    （1）根据韦达定理，求，代入不等式，解分式不等式；

    （2）原不等式可化为，时，解不等式；当时，方程的两根为，讨论两根的大小关系，解不等式.

    解：（1）由韦达定理知，

    不等式为，移项整理得

    ，解得

    不等式的解集为

    （2）由题意得，原不等式可化为

    （1）当时，原不等式的解集为

    （2）当时，方程的两根为

    ①当时，即时，原不等式的解集为

    ②当时，即时，原不等式的解集为

    ③当时，即时，原不等式的解集为

    综上所述，当时，原不等式的解集为；当0时，原不等式的解集为；当时，原不等式的解集为；当时，原不等式的解集为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在竖直坐标平面中，从坐标原点出发以同一初速度和不同的发射角（即发射方向与轴正向之间的夹角）射出的质点（不计质点的大小），在重力（设重力加速度为）的作用下运动轨迹是抛物线，所有这些抛物线组成一个抛物线族（即抛物线的集合）.若两条抛物线在同一个交点处的切线互相垂直，则称这个交点为正交点.证明：此抛物线族的所有正交点的集合是一段椭圆弧，并求出这个椭圆弧的方程（包括变量的取值范围），再画出它的草图.注. 抛物线在其上的点处的切线的斜率为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，圆的方程为，若直线上至少存在一点，使得以该点为圆心，1为半径的圆与圆有公共点，则的最大值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为常数），方程有两个实根3和4，

    （1）求的解析式；

    （2）设，解关于x的不等式；

    （3）已知函数是偶函数，且在上单调递增，若不等式在任意上恒成立，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的参数方程为（为参数），直线的参数方程为（为参数），设与的交点为，当变化时， 的轨迹为曲线.

    （1）写出的普遍方程及参数方程；

    （2）以坐标原点为极点， 轴正半轴为极轴建立极坐标系，设曲线的极坐标方程为， 为曲线上的动点，求点到的距离的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，多面体中， 是正方形， 是梯形， ， ， 平面且， 分别为棱的中点．

    （Ⅰ）求证：平面平面；

    （Ⅱ）求平面和平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A＝{x|1≤x≤3}，B＝{x|x＞2}．

    （Ⅰ）分别求A∩B，（RB）∪A；

    （Ⅱ）已知集合C＝{x|1＜x＜a}，若CA，求实数a的取值集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】100个火柴盒，标号为1至100.我们可以问其中任15个盒子总共含有的火柴为奇数或偶数.至少要问几个问题才能确定1号盒子里的火柴数的奇偶性？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车站在春运期间为了了解旅客购票情况，随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间（以下简称为购票用时，单位为min），下面是这次调查统计分析得到的频率分布表和频率分布直方图.

    频率

    分组

    频数

    10

    0.10

    10

    ②

    ①

    0.50

    30

    0.30

    合计

    100

    1.00

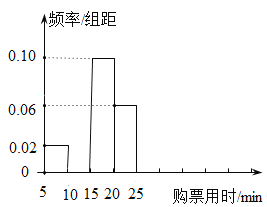
    解答下列问题：

    （1）在表中填写出缺失的数据并补全频率分布直方图；

    （2）估计旅客购票用时的平均数.

    查看答案和解析>>

    同步练习册答案